A rope of length (π2+1) R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is λ . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass (M0) of a block that can be tied to the end B of the rope so that the string does not break.
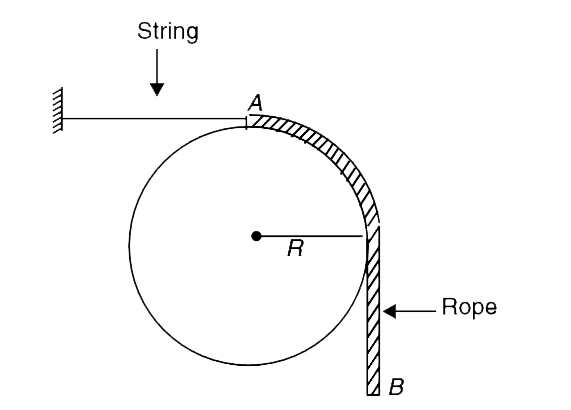
The correct Answer is:M0=λR(π2−1)
Step by step video, text & image solution for A rope of length ((pi)/(2) + 1) R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is lambda . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass (M_(0)) of a block that can be tied to the end B of the rope so that the string does not break. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle is acted upon by a force for 1 second whose X component remains constant at Fx=30N but y and z components vary with time as shown in the graph. Calculate the magnitude of change in momentum of the particle in 1 s. What angle does the change in momentum (Δ→P) make with X axis ?

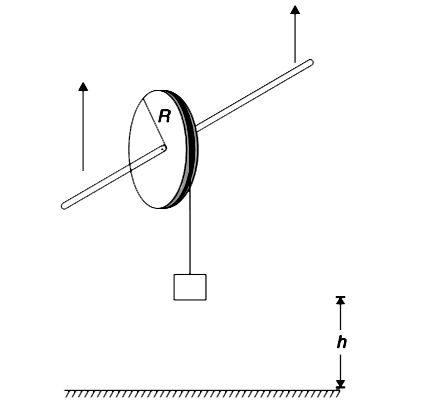
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA uniform of rope length L and mass M is placed on a smooth fixed wedge as shown. Both ends of rope are at same horizontal level. The rope is initially released from rest, then the magnitude of initial acceleration of rope is.
View SolutionA uniform rope of length (piR)/(2) has been placed on fixed cylinder of radius R as shown in the fig. One end of the rope is at the top of the cylinder. The coefficient of friction between the rope and the cylinder is just enough to prevent the rope from sliding. Mass of the rope is M. (a) At what position, the tension in the rope is maximum? (b) Calculate the value of maximum tension in the rope.
View SolutionA circular rope of weight W and radius r=R/2 is resting on a smooth sphere of radius R The tension in rope is
View SolutionA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Acceleration (A) of the rope is
View SolutionA rope of length of 2m is tied between two ends . If the speed of transverse waves propagating in the rope is 4 m s^(-1) and the tension in the rope is 2 N , find the mass of the rope is C.G.S units .
View SolutionA uniform rope of length L rests on a smooth plane. One end of the rope is pulled with a force F. what is the tension in the rope at a distance l from that end ?
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'l' from that end is
View SolutionA straight rope of length 'L' is kept on a frictionless horizontal surface and a force 'F' is applied to one end of the rope in the direction of its length and away from that end. The tension in the rope at a distance 'I from that end is 9
View Solutionएक 25 cm त्रिज्या तथा 1 kg द्रव्यमान वाले गोले को एक नगण्य द्रव्यमान तथा 40 cm लम्बाई वाली रस्सी से लटकाया गया है तो रस्सी में तनाव होगा
View SolutionA rope of length 5 m has uniform mass per unit length. lambda = 2 kg/m The rope is pulled by a constant force of 10N on the smooth horizontal surface as shown in figure The tension in the rope at x = 2 m from polit A is
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View Solution
