A simple pendulum 4 m long swings with an amplitude of 0.2 m. What is its acceleration at the ends of its path? (g = )
Zero
The correct Answer is:C
To find the acceleration of a simple pendulum at the ends of its path, we can follow these steps:
1. Identify the Given Values:
- Length of the pendulum (L) = 4 m
- Amplitude (A) = 0.2 m
- Acceleration due to gravity (g) = 10 m/s²
2. Understand the Concept:
- The acceleration of a simple pendulum is maximum at the extreme positions (the ends of its path).
- The formula for the maximum acceleration (a_max) at the extreme position is given by:
amax=ω2⋅A
- Where ω is the angular frequency.
3. Calculate the Angular Frequency (ω):
- The angular frequency ω can be calculated using the formula:
ω=√gL
- Substituting the values:
ω=√10m/s24m=√2.5rad/s
4. Calculate ω2:
- Now, square ω:
ω2=2.5rad2/s4
5. Calculate Maximum Acceleration (a_max):
- Substitute ω2 and amplitude (A) into the maximum acceleration formula:
amax=ω2⋅A=2.5⋅0.2
- Calculate:
amax=0.5m/s2
6. Final Result:
- The maximum acceleration at the ends of the path is:
amax=0.5m/s2
Summary:
The acceleration at the ends of the path for the simple pendulum is 0.5 m/s².
- Length of the pendulum (L) = 4 m
- Amplitude (A) = 0.2 m
- Acceleration due to gravity (g) = 10 m/s²
- The acceleration of a simple pendulum is maximum at the extreme positions (the ends of its path).
- The formula for the maximum acceleration (a_max) at the extreme position is given by:
amax=ω2⋅A
- Where ω is the angular frequency.
- The angular frequency ω can be calculated using the formula:
ω=√gL
- Substituting the values:
ω=√10m/s24m=√2.5rad/s
- Now, square ω:
ω2=2.5rad2/s4
- Substitute ω2 and amplitude (A) into the maximum acceleration formula:
amax=ω2⋅A=2.5⋅0.2
- Calculate:
amax=0.5m/s2
- The maximum acceleration at the ends of the path is:
amax=0.5m/s2
The acceleration at the ends of the path for the simple pendulum is 0.5 m/s².
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A simple pendulum of length 1m is attached to the ceiling of an elevator which is accelerating upward at the rate of 1m/s2. Its frequency is approximately :-
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘ true
false
View SolutionA simple pendulum with a bob of mass m swings with an angular amplitude of 40∘. When its angular displacement is 20∘, the tension in the string is greater than mgcos20∘
View SolutionA tennis ball is dropped on the floor from a height of 20m. It rebounds to a height of 5m. If the ball was in contact with the floor for 0.01s. What was its average acceleration during contact? (g=10m/s2)
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
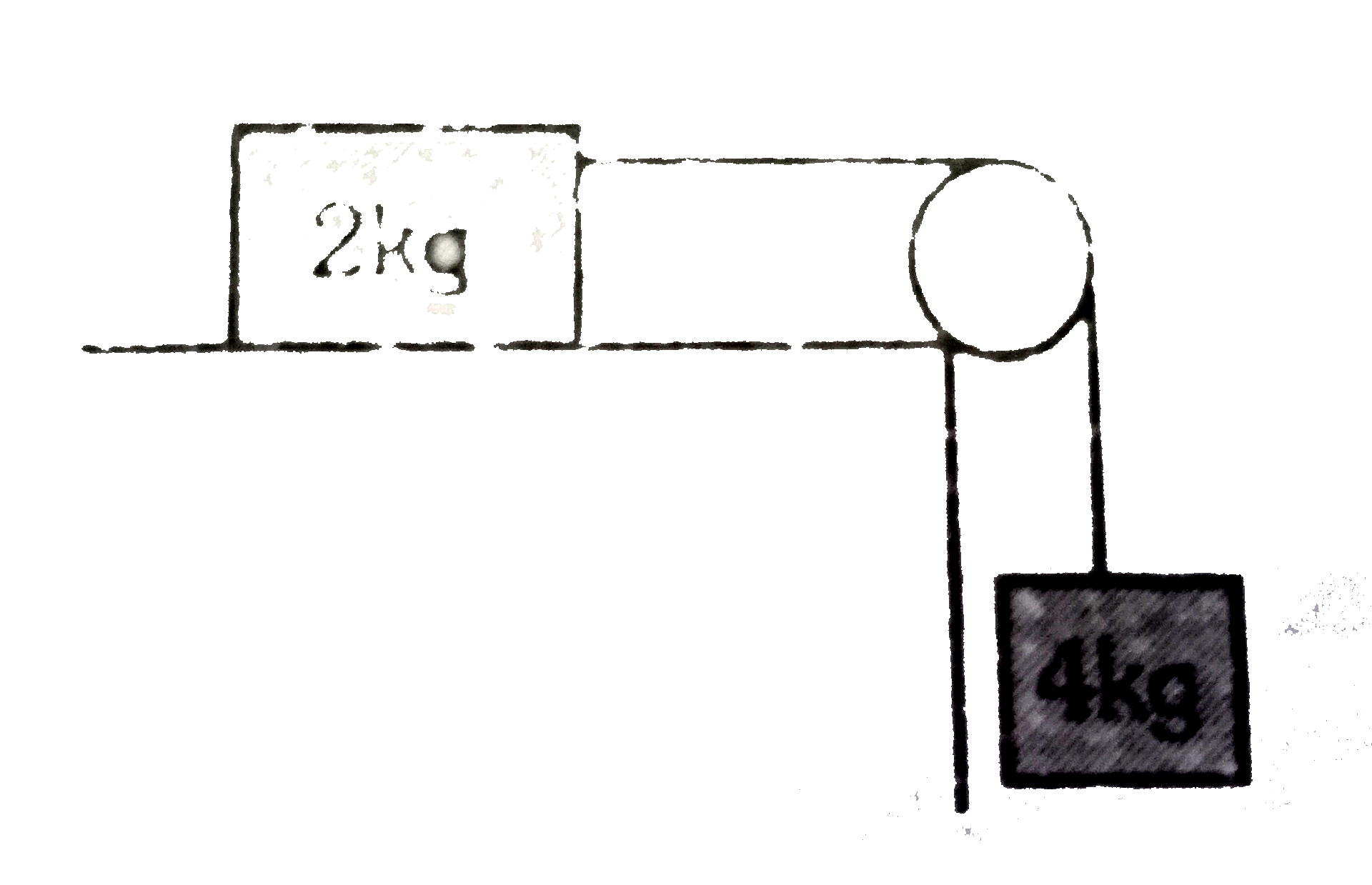
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt

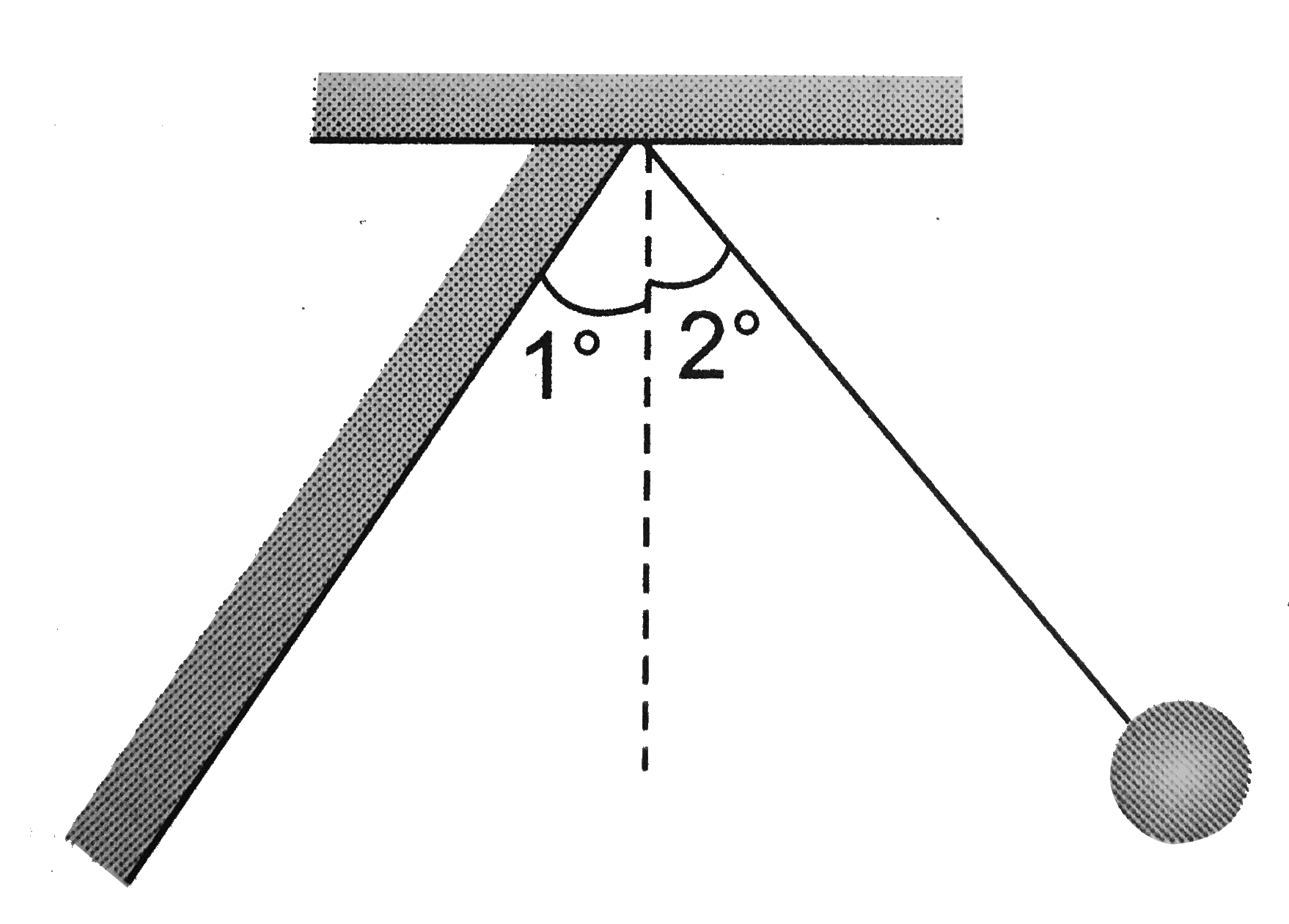
View SolutionA simple pendulum of length 1m is allowed to oscillate with amplitude 2∘. it collides at T to the vertical its time period will be (use g=π2)
View SolutionA fixed pulley of radius 20 cm and moment of inertia 0.32 kg.m2 about its axle has a massless cord wrapped around its rim. A mass M of 2 kg is attached to the end of the cord. The pulley can rotate about its axis without any friction. The acceleration of the mass M is :- (Assuming g=10m/s2)

View SolutionThe bob of a simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the stirng at this instant.
View Solution
