A simple pendulum oscillates slightly above a large horizontal metal plate. The bob is given a charge. The time period
has no reffect, whatever be the nature of charge
always decreases, whatever be the nature of charge
always increases, whatever be the nature of charge
a increases or decreases depending upon the nature of charge.
The correct Answer is:B
To solve the problem of the time period of a simple pendulum oscillating above a large horizontal metal plate with a charged bob, we can follow these steps:
Step 1: Understand the System
- A simple pendulum consists of a bob suspended from a fixed point, which can swing back and forth.
- In this case, the bob is charged, and it is positioned above a large horizontal metal plate.
Step 2: Analyze the Forces Acting on the Bob
- The forces acting on the bob include:
1. The gravitational force (weight) acting downwards, Fg=mg, where m is the mass of the bob and g is the acceleration due to gravity.
2. An electrostatic force due to the interaction between the charged bob and the induced charges on the metal plate. Since the bob is positively charged, the plate will induce a negative charge on its upper surface, resulting in an attractive force.
Step 3: Determine the Effective Gravitational Force
- The effective gravitational force acting on the bob can be expressed as:
Feffective=mg+Fq
where Fq is the electrostatic force acting upwards.
Step 4: Define the Effective Acceleration
- The effective acceleration geffective can be defined as:
geffective=g+Fqm
This indicates that the effective gravitational acceleration is increased due to the additional upward force from the electrostatic attraction.
Step 5: Write the Formula for the Time Period
- The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum. However, since we have an effective gravitational acceleration, we replace g with geffective:
T=2π√Lgeffective
Step 6: Analyze the Effect of Increased geffective
- Since geffective>g due to the additional force Fq, we can conclude that:
T=2π
⎷Lg+Fqm
This implies that as geffective increases, the time period T will decrease.
Step 7: Conclusion
- Regardless of whether the bob is positively or negatively charged, the presence of the metal plate will always increase the effective gravitational force acting on the bob, leading to a decrease in the time period of oscillation.
Final Answer
The time period of the pendulum will decrease when the bob is charged and oscillating above the metal plate.
---
- A simple pendulum consists of a bob suspended from a fixed point, which can swing back and forth.
- In this case, the bob is charged, and it is positioned above a large horizontal metal plate.
- The forces acting on the bob include:
1. The gravitational force (weight) acting downwards, Fg=mg, where m is the mass of the bob and g is the acceleration due to gravity.
2. An electrostatic force due to the interaction between the charged bob and the induced charges on the metal plate. Since the bob is positively charged, the plate will induce a negative charge on its upper surface, resulting in an attractive force.
- The effective gravitational force acting on the bob can be expressed as:
Feffective=mg+Fq
where Fq is the electrostatic force acting upwards.
- The effective acceleration geffective can be defined as:
geffective=g+Fqm
This indicates that the effective gravitational acceleration is increased due to the additional upward force from the electrostatic attraction.
- The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum. However, since we have an effective gravitational acceleration, we replace g with geffective:
T=2π√Lgeffective
- Since geffective>g due to the additional force Fq, we can conclude that:
T=2π
⎷Lg+Fqm
This implies that as geffective increases, the time period T will decrease.
- Regardless of whether the bob is positively or negatively charged, the presence of the metal plate will always increase the effective gravitational force acting on the bob, leading to a decrease in the time period of oscillation.
The time period of the pendulum will decrease when the bob is charged and oscillating above the metal plate.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A spring-block system undergoes vertical oscillations above a large horizontal metal sheet with uniform positive charge. The time period of the oscillations is T. If the block is given a charge Q, its time period of oscillation will be
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
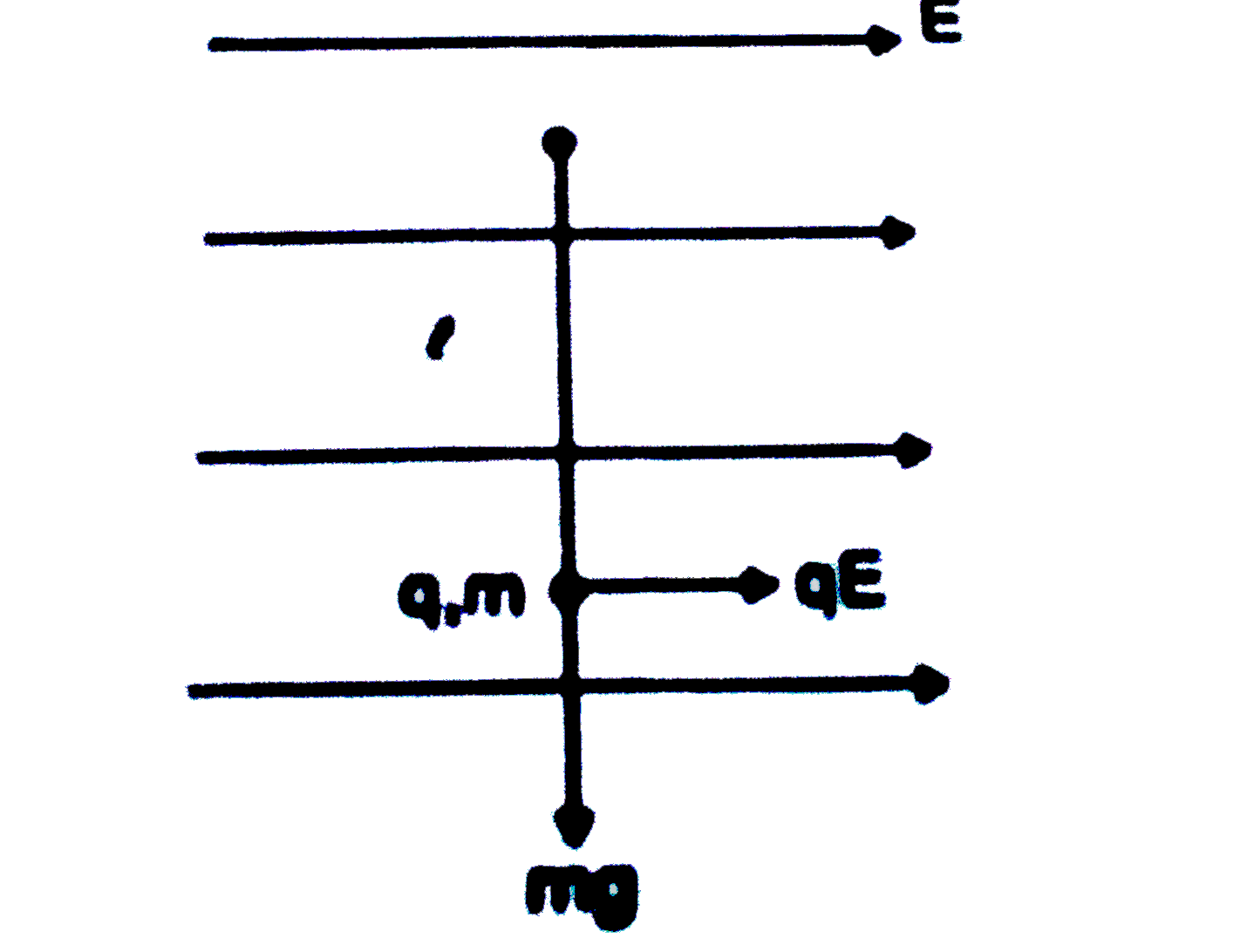
View SolutionThe bob of a simple pendulum of length /has a positive charge q on it. The pendulum is fixed to a horizontally oriented positively charged sheet as shown in the figure. The time period of the small oscillations of simple pendulum is
View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View SolutionAn oscillating simple pendulum is kept in a lift which is accelerating upwards. Will there be any change in the time period ?
View SolutionA simple pendulum of length 40 cm oscillates with an angular amplitude of 0.04 rad. Find a. the time period b. the linear amplitude of the bob, c. The speed of the bob when the string makes 0.02 rad with the vertical and d. the angular acceleration when the bob is in momentarily rest. Take g=10ms−2.
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionA simple pendulum completes 40 oscillations in one minute. Find its time period .
View SolutionA simple pendulum has time period T The bob is given negative charge and surface below it is given positive change new time period will be
View SolutionIf a simple pendulum oscillates with an amplitude of 50 mm and time period of 2 sec, then its maximum velocity is
View Solution
