A small ball of mass m is projected with a minimum horizontal velocity v0 on a smooth wedge of mass M so that it will reach the highest point of the wedge. Find the value of v0


if the ball reaches at point P, the velocity of the ball with respect to wedge should be √gR
using work energy theorem from centre of mass frame at A and the highest point P ltbr Wext+W∫+0=(△K)−(cm)
Wgravity=(△K)CM
−mg(2R)=[12μv2rel]final−[12μv2rel]initial
−mg2R=12μ(V+v)2−12μv20..............i
μ=(mMm+M) and v=√gR
As there is no external forces acting on the system in horizontal direction. the linear momentum of the system should be conserved.
i.e. mv0=m(V−v)+MV
V=m(v0+v)(m+M) ............ii
from eqn i and ii we get
⇒v0=√(5+4mM)gR
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.223videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
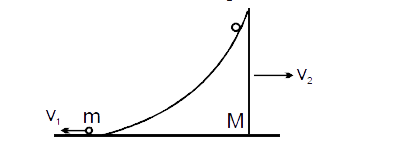
A particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
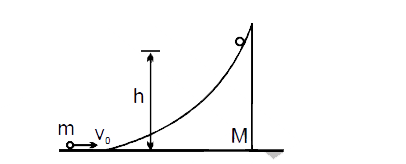
The final velocity of the wedgev2 isView SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
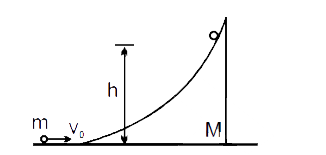
Choose the correct statement related to the wedge MView Solution
Knowledge Check
- Question 1 - Select One
A shell of mass m is moving horizontally with velocity v0 and collides with the wedge of mass M just above points A, as shown in the figure. As a consequences, wedge starts to move towards left and the shell returns with a velocity in xy-plance. The principle of conservation of momentum can be applied for
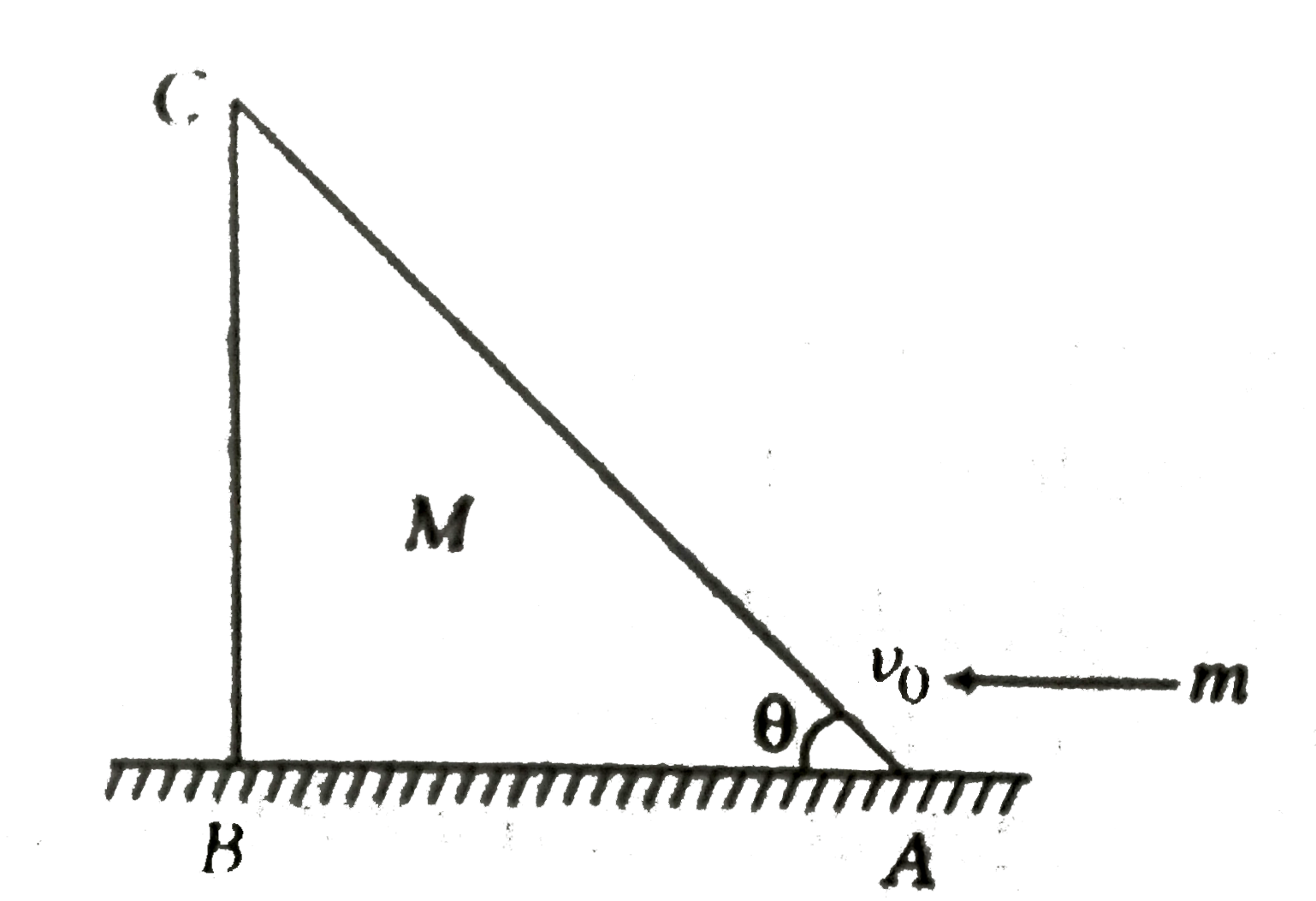 Asystem (m + M) along any directionBsystem (m+M) along verticalCsystem (m + M) horizontallyDNone of the above
Asystem (m + M) along any directionBsystem (m+M) along verticalCsystem (m + M) horizontallyDNone of the above
A particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
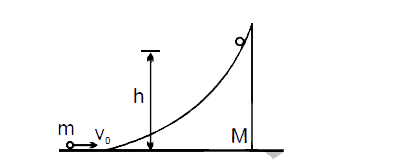
When the particle has risen to a height h on the wedge, then choose the correct alternative(s)View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
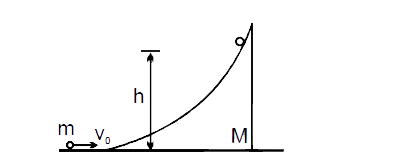
Suppose the particle when reaches the horizontal surfaces, its velocity with respect to ground is v1 and that of wedge is v2. Choose the correct statement (s)
 View Solution
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
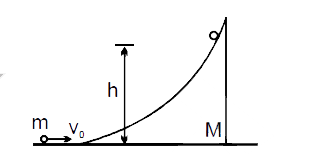
Choose the correct statement(s) related to particle mView SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
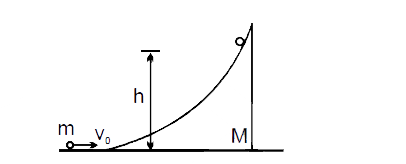
The maximum height h attained by the particle isView SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
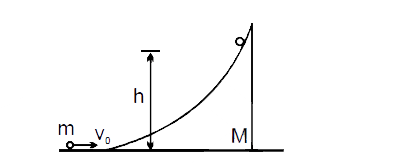
Identify the correct statement(s) related to the situation when the particle starts moving downwardView SolutionA shell of mass m is moving horizontally with velocity v0 and collides with the wedge of mass M just above points A, as shown in the figure. As a consequences, wedge starts to move towards left and the shell returns with a velocity in xy-plance. The principle of conservation of momentum can be applied for
 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View Solution

