A smooth massless string passes over a smooth fixed pulley. Two masses m1andm2(m1>m2) are tied at the two ends of the string. The masses are allowed to move under gravity starting from rest. The acceleration of the two masses is Solution in Bengali
(m1+m2)g
(m1−m2)m1+m2g
(m1−m2)g
(m1+m2)2m1−m2g
If a is the acceleration of the two masses and T is the tension in the two sides of the string, then
m1g−T=m1a (1)
T−m2g=m2a …(2)
Now from equations (1) and (2), we get,
a = (m1−m2)m1+m2g
Therefore, total external force
=(m1+m2)a=(m1−m2)g
The option c is correct.

Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (AIPMT)3videos
NEWTON'S LAWS OF MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS (NEET)3videos
NEWTON'S LAWS OF MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - EXAMINATION ARCHIVE WITH SOLUTIONS(WBCHSE)17videos
NEWTON'S LAWS OF MOTION
- BOOK - CHHAYA PUBLICATIONCHAPTER - NATURE OF VIBRATIONEXERCISE - EXERCISE (CBSE SCANNER)2videos
NATURE OF VIBRATION
- BOOK - CHHAYA PUBLICATIONCHAPTER - NEWTONIAN GRAVITATION AND PLANETARY MOTIONEXERCISE - CBSE SCANNER19videos
NEWTONIAN GRAVITATION AND PLANETARY MOTION
Similar Questions
The force F acting on a particle of mass m is indicated by the force-time graph shown below. The change in momentum of the particle over the time interval from zero to 8 s is
 03:50View Solution
03:50View SolutionA girl jumps down from a moving bus, along the direction of motion of the bus, tilting slightly forward. She falls on
(a) sheet of ice03:11View SolutionA block of mass M is pulled along a frictionless horizontal suface by a rope of mass m by applying a horizontal force F at the other end of the rope. The force exerted by the rope on the block is
03:01View Solution(i) What do you mean by resonance ? (ii) Mention any two uses of its from your daily life.
01:12View SolutionWhat is the reason for absence of atmosphere in some planets?
08:18View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
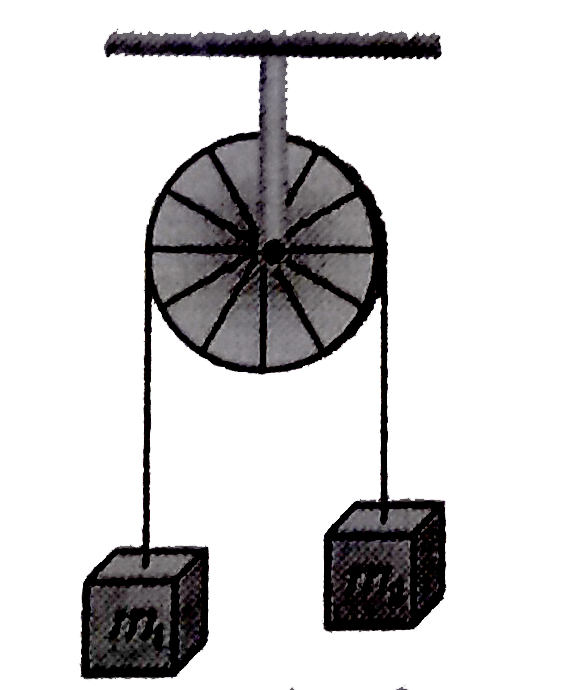 05:23View Solution
05:23View SolutionTwo blocks of mass m_(1)"and"m_(2) are connected by light inextensible string passing over a smooth fixed pulleuy of negligible mass. The acceleration of the centre of mass of the system when blocks move under gravity is :
01:40View SolutionFind the acceleration of masses m1 and m2 moving down the smooth incline plane. The string and the pulley are masseless and frictionless.
04:00View SolutionTwo masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 02:13View Solution
02:13View SolutionTwo masses m1andm2 are connected to the end of a string passing over a smooth pulley . The magnitude of tension in the string is T and the masses are moving with magnitude of acceleration a . If the masses are interchanged , then
06:27View SolutionTwo masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
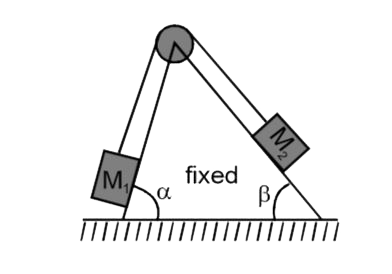 03:58View Solution
03:58View SolutionFig. shows a block of mass m1 resting on a smooth surface. It is connected to a mass m2 by a string passing over a massless and frictionaless pulleys m2>m1. The acceleration of the hanging mass m2 is :
 View Solution
View SolutionTwo masses m_(1) and m_(2) ( m_(2) gt m_(1)) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
02:12View SolutionTwo masses m_(1) and m_(2) are connected to the ends of string passing over a pulley. Find the tension and the acceleration associated.
10:52View Solution

