
A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC?
At B, total kinetic energy =mgh
Here, m= mass of ball
The ratio of ratational to translational kinetic energy would be.
KRKT=25⇒∴KR=27mgh and KT=57mgh
In portiona BC, friction is absent. therefore, rotational kinetic energy will remain constant and translational kinetic energy will convert into potential energy. Hence, if H be the height to which ball climbs in BC, then
mgH=KT or mgH=57mgh or H=57h
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Example1videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A hollow spherical ball rolls down on a parabolic path AB from a height 'h' as shown in the figure. Path AB is rough enough to prevent slipping of ball and path BC is frictionless. The height to which the ball will climb in BC is
 View Solution
View SolutionA solid sphere is released from rest from the top of a curved surface as shown in figure. Half portion of surface is rough and another half is smooth. If sphere is released from rough side, then the maximum height attained by it on smooth side is (Rough surface has sufficient friction to roll the body)
View SolutionA small ball is rolled with speed u from piont A along a smooth circular track as shown in figure. If x=3R, then

What is the minimum value of x for which the ball can reach the point of projection after reaching C?View SolutionA smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane.
a. If e=0, find the speed of the ball just after leaving the inclined plane 1.
b. If the particle mioves horizontally just after the collision find e.
 View Solution
View SolutionA small ball of mass m is connected by an inextensible massless string of length with an another ball of mass M=4m. They are released with zero tension in the string from a height h as shown in the figure. Find the time when the string becomes taut for the first time after the mass M collides with the ground. Take all collisions to be elastic.
 View Solution
View SolutionA solid sphere rolls down a parabolic path , whose vertical dimension is given by y=kx2 and base of the parabola is at x = 0 . During the fall the sphere does not slip, but beyond the base the climb is frictionless. If the sphere falls through a height h, the height above the base that it would climb is
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.
 View Solution
View SolutionA ball of mass m is allowed to roll down the wedge of mass M=2m as shown in the figure. What is the displacement of wedge (in m) when the ball reaches from A to B? Take θ=45∘,h=1m,d=4m
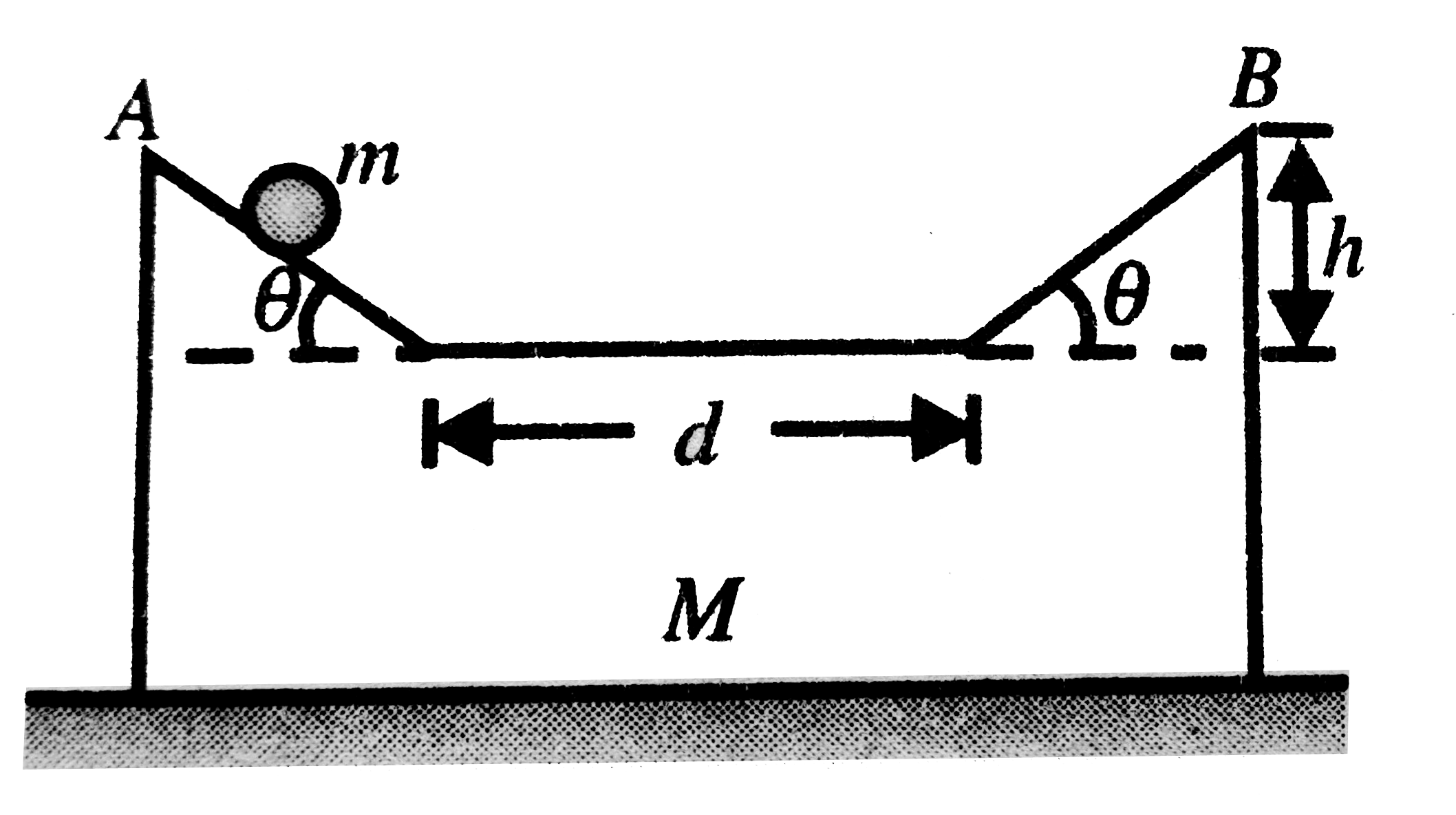 View Solution
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
View SolutionTwo identical uniform solid spherical balls A and B of mass m each are placed on a the fixed wedge as shown in figure. Ball B is kept at rest and it is released just before two balls collides. Ball A rolls down without slipping on inclined plane and collide elastically with ball B. The kinetic energy of ball A just after the collision with ball B is:
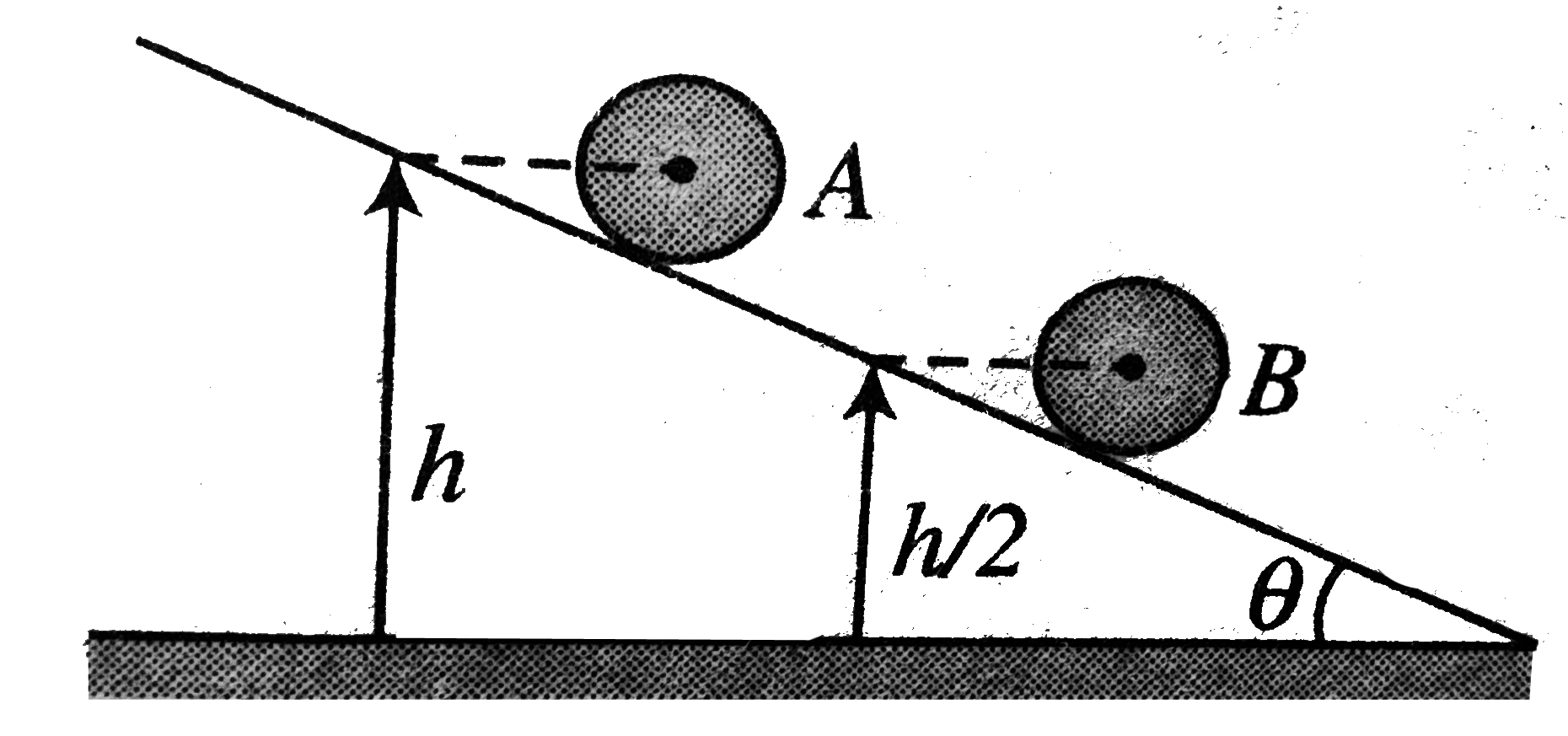 View Solution
View Solution

