A solid sphere of radius R and mass density ρ is surrounded by another outer sphere of density 2ρ. Let EP is gravitational field at P and EQ is at Q. If the ratio of EQ/EP=3k/4. Find the value of k.

Step by step video & image solution for A solid sphere of radius R and mass density rho is surrounded by another outer sphere of density 2 rho. Let E_(P) is gravitational field at P and E_(Q) is at Q. If the ratio of E_(Q)//E_(P)=3k//4. Find the value of k. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two uniform solid spheres of same materical and same radius are touching each other density is 'ρ' then find out gravitational force between them .
View SolutionConsider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View Solution
Knowledge Check
A system consits of a uniformly charged sphere of radius R and a surrounding medium filled by a charge with the volume density ρ=αr, where α is a positive constant and r is the distance from the centre of the sphere. Find the charge of the sphere for which the electric field intensity E outside the sphere is independent of R.
Aα2ε0B2αε0C2παR2DNone of theseThe acceleration due to gravity g and density of the earth ρ are related by which of the following relations? (where G is the gravitational constant and RE is the radius of the earth)
Aρ=4πGRE3gBρ=3g4πGRECρ=3G4πgREDρ=4πgRE3G
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
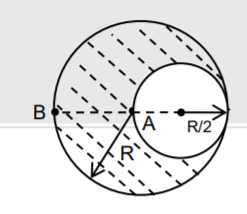
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionFor an infinitely long solid cylinder of radius R having a uniform density , the gravitational field at a distance r1 is E1 and at a distance r2 is E2 , then
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
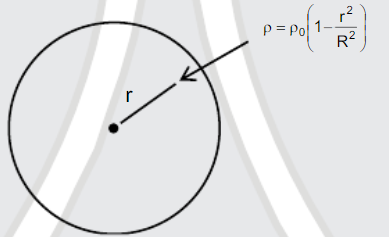
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
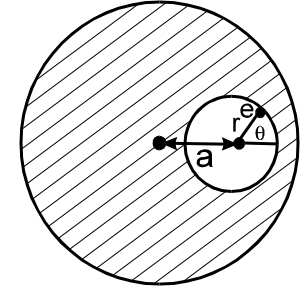
View SolutionA cavity of radius r is present inside a fixed solid dielectric sphere of radius R, having a volume charge density of ρ. The distance between the centres of the sphere and the cavity is a. An electron is released inside the cavity at an angle θ=450 as shown. The electron (of mass m and charge –e) will take (P√2mrε0eaρ)1/2 time to touc the sphere again. Neglect gravity. find the value of P:
View Solution
