A sphere is released on a smooth inclined plane from the top. When it moves down, its angular momentum is
conserved about every point
conserved about the point of contact only
conserved about the centre of the sphere only
conserved about any point on a line parallel to the inclined plane and passing through the centre of the ball
The correct Answer is:D
To solve the problem of the angular momentum of a sphere released on a smooth inclined plane, we will follow these steps:
Step 1: Understand the System
We have a sphere released from the top of a smooth inclined plane. The plane is smooth, which means there is no friction acting on the sphere as it rolls down.
Step 2: Identify Forces Acting on the Sphere
When the sphere is on the inclined plane, the forces acting on it are:
- The gravitational force (weight) mg, acting vertically downwards.
- The normal force N, acting perpendicular to the surface of the inclined plane.
Step 3: Break Down the Weight into Components
The weight can be resolved into two components:
- A component parallel to the incline: mgsinθ
- A component perpendicular to the incline: mgcosθ
Step 4: Analyze Torque
To determine if angular momentum is conserved, we need to analyze the torque about specific points. The condition for conservation of angular momentum is that the net torque about a point must be zero.
1. About the Center of Mass:
- The forces mgsinθ and mgcosθ act through the center of mass of the sphere.
- Since the torque due to these forces about the center of mass is zero, angular momentum is conserved about the center of mass.
2. About the Point of Contact:
- The torque due to the weight component mgsinθ will not be zero because it does not pass through the point of contact.
- Therefore, angular momentum is not conserved about the point of contact.
3. About Any Point Parallel to the Inclined Plane:
- For any point along a line parallel to the inclined plane and passing through the center of the sphere, the torque due to mgsinθ will be zero, as it acts through that line.
- However, the torque due to mgcosθ will still be present, which means angular momentum is not conserved about all such points.
Step 5: Conclusion
The angular momentum of the sphere is conserved about its center of mass. Therefore, the correct answer to the question is:
The angular momentum of the sphere is conserved about its center of mass.
Final Answer:
Conserved about the center of the sphere only.
We have a sphere released from the top of a smooth inclined plane. The plane is smooth, which means there is no friction acting on the sphere as it rolls down.
When the sphere is on the inclined plane, the forces acting on it are:
- The gravitational force (weight) mg, acting vertically downwards.
- The normal force N, acting perpendicular to the surface of the inclined plane.
The weight can be resolved into two components:
- A component parallel to the incline: mgsinθ
- A component perpendicular to the incline: mgcosθ
To determine if angular momentum is conserved, we need to analyze the torque about specific points. The condition for conservation of angular momentum is that the net torque about a point must be zero.
- The forces mgsinθ and mgcosθ act through the center of mass of the sphere.
- Since the torque due to these forces about the center of mass is zero, angular momentum is conserved about the center of mass.
- The torque due to the weight component mgsinθ will not be zero because it does not pass through the point of contact.
- Therefore, angular momentum is not conserved about the point of contact.
- For any point along a line parallel to the inclined plane and passing through the center of the sphere, the torque due to mgsinθ will be zero, as it acts through that line.
- However, the torque due to mgcosθ will still be present, which means angular momentum is not conserved about all such points.
The angular momentum of the sphere is conserved about its center of mass. Therefore, the correct answer to the question is:
Conserved about the center of the sphere only.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A body of mass m and radius r is released from rest along a smooth inclined plane of angle of inclination θ. The angular momentum of the body about the instantanoues point contact after a time t from the instant of release of equal is :
View SolutionA block is released from the top of a smooth inclined plane of inclination θ as shown in figure. Let υ be the speed of the particle after travelling a distance s down the plane. Then which of the following will remain constant ?
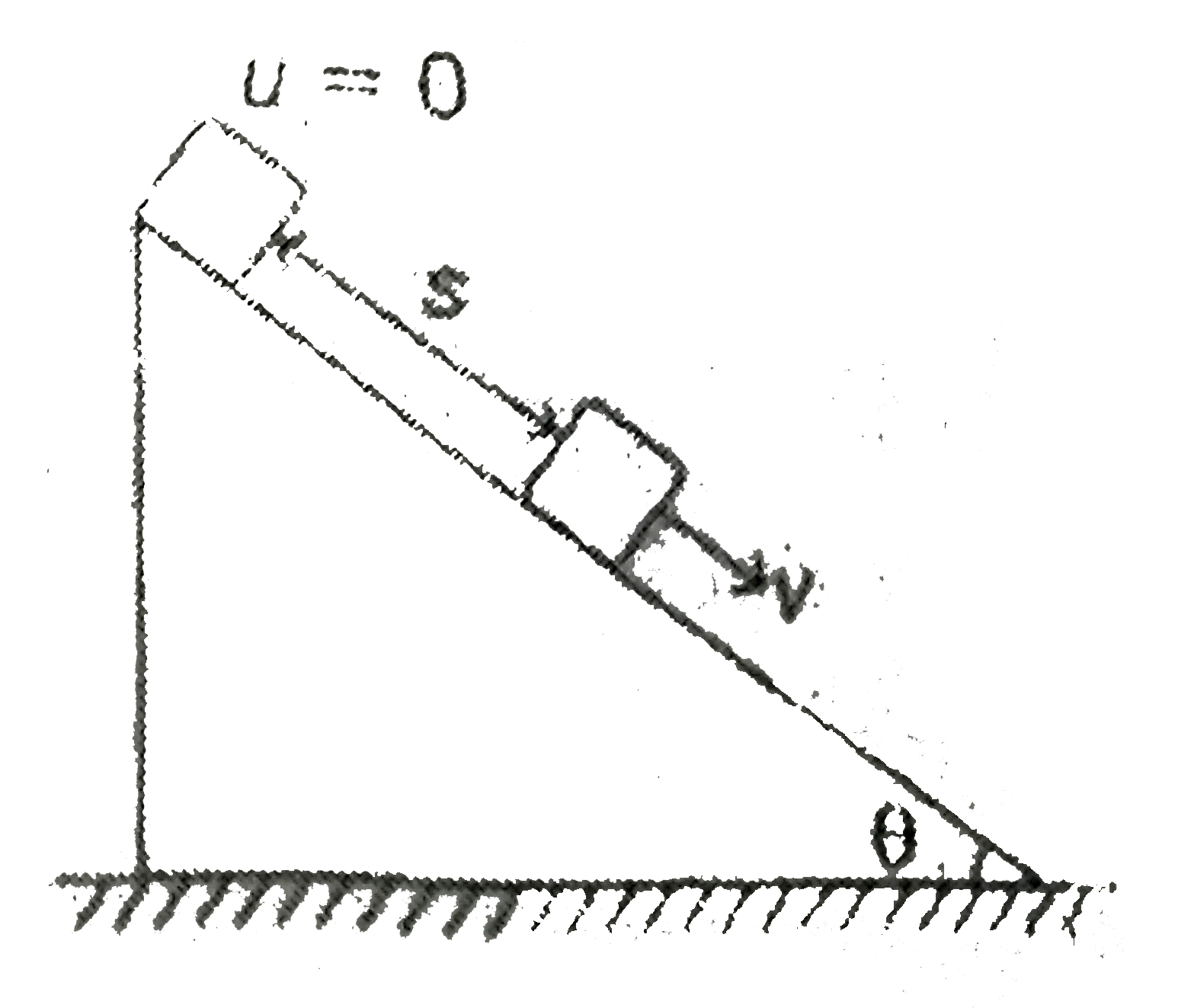 View Solution
View SolutionA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then
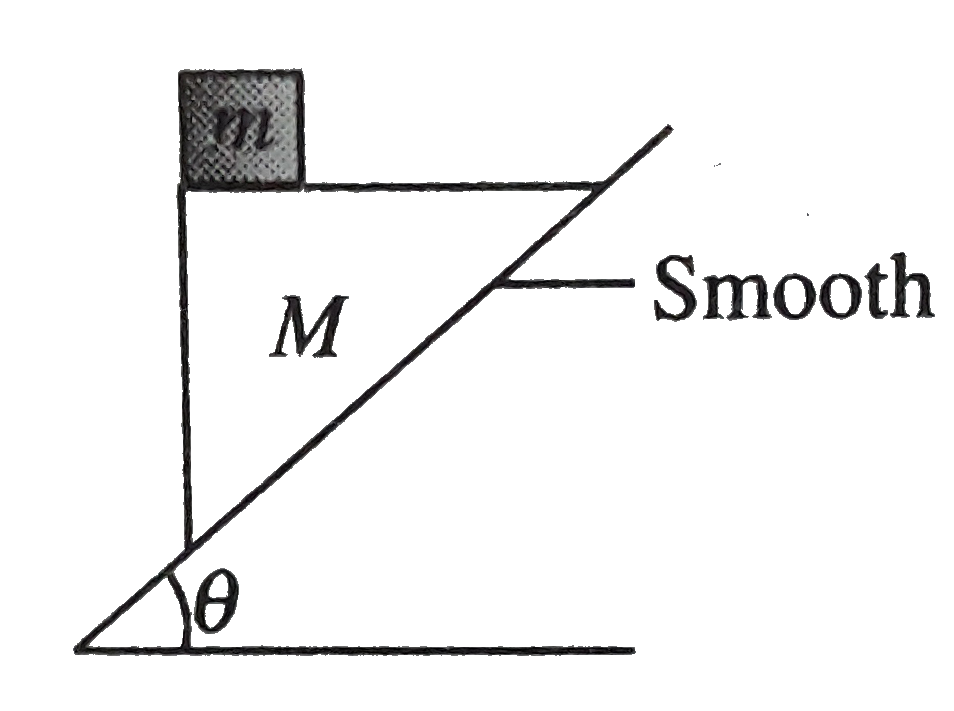 View Solution
View SolutionSTATEMENT-1: A ball of mass m is released from the top of a smooth inclined plane. At the same time another ball of same mass allowed to fall freely from same height. When both balls reaches the bottom of the plane, momentum will not be equal
because
STATEMENT-2: Momentum depends on the direction of velocity as well as its magnitude.View SolutionA spherical object of mass m and radius R is released from the top of a smooth inclined plane of height h and angle of inclination is 37° . The radius of gyration of the object is K. The speed of object at the bottom of inclined plane is
View SolutionA solid sphere is roilling down on inclined plane from rest and rectangular block of same mass is also slipping down simultaneously from rest on the same plane. Then:
View SolutionA particle of mass m comes down on a smooth inclined plane from point B at a height of h from rest. The magni-tude of change in momentum of the particle between position A (just before arriving on horizontal surface) and C (assuming the angle of inclination of the plane as θ with respect to the horizontal) is
 View Solution
View SolutionA hollow sphere is released from top of an inclined plane of inclination 30º and length of inclined plane is /. If sphere rolls without slipping then its speed at bottom is
View SolutionA block slides down a smooth inclined placne when released from the top, while another falls freely from the same point. Which of the following is/are correct ?
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View Solution
