A sphere rolls on a horizontal surface. Is there any point of the sphere which has a vertical velocity?
To determine if there is any point on a rolling sphere that has a vertical velocity, we can analyze the motion of the sphere step by step.
1. Understanding the Rolling Motion:
A sphere rolling on a horizontal surface has both translational and rotational motion. The center of mass of the sphere moves with a linear velocity V, and the sphere rotates about its center with an angular velocity ω.
2. Relating Linear and Angular Velocity:
The relationship between the linear velocity V and the angular velocity ω is given by the equation:
V=rω
where r is the radius of the sphere.
3. Velocity at Different Points on the Sphere:
The velocity of any point on the sphere can be expressed as the sum of the translational velocity of the center of mass and the rotational velocity due to the sphere's rotation. For a point on the surface of the sphere, the velocity →v can be represented as:
→v=→Vcm+→vrot
where →Vcm is the velocity of the center of mass and →vrot is the rotational velocity at that point.
4. Identifying Points on the Sphere:
- The point at the bottom of the sphere (the point in contact with the ground) has a velocity of zero because it is instantaneously at rest.
- The point at the top of the sphere moves with a velocity of 2V (the sum of the translational velocity and the rotational velocity).
5. Analyzing Vertical Velocity:
The vertical velocity of a point on the sphere can be determined by considering the vertical component of the velocity at different points:
- At the top of the sphere, the vertical component is directed upwards.
- At the bottom of the sphere, the vertical component is zero.
- At points along the equator, the vertical component can be both positive and negative depending on the position.
6. Conclusion:
Yes, there are points on the sphere, particularly at the equator, where the sphere has a vertical velocity component. The points on the equator will have vertical velocities that depend on the sphere's rotation and the direction of motion.
A sphere rolling on a horizontal surface has both translational and rotational motion. The center of mass of the sphere moves with a linear velocity V, and the sphere rotates about its center with an angular velocity ω.
The relationship between the linear velocity V and the angular velocity ω is given by the equation:
V=rω
where r is the radius of the sphere.
The velocity of any point on the sphere can be expressed as the sum of the translational velocity of the center of mass and the rotational velocity due to the sphere's rotation. For a point on the surface of the sphere, the velocity →v can be represented as:
→v=→Vcm+→vrot
where →Vcm is the velocity of the center of mass and →vrot is the rotational velocity at that point.
- The point at the bottom of the sphere (the point in contact with the ground) has a velocity of zero because it is instantaneously at rest.
- The point at the top of the sphere moves with a velocity of 2V (the sum of the translational velocity and the rotational velocity).
The vertical velocity of a point on the sphere can be determined by considering the vertical component of the velocity at different points:
- At the top of the sphere, the vertical component is directed upwards.
- At the bottom of the sphere, the vertical component is zero.
- At points along the equator, the vertical component can be both positive and negative depending on the position.
Yes, there are points on the sphere, particularly at the equator, where the sphere has a vertical velocity component. The points on the equator will have vertical velocities that depend on the sphere's rotation and the direction of motion.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer13videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
Similar Questions
A sphere cannot roll on
View SolutionA sphere cannot roll on
View SolutionA solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity vm/s. If it is to climb the inclined surface then v should be :
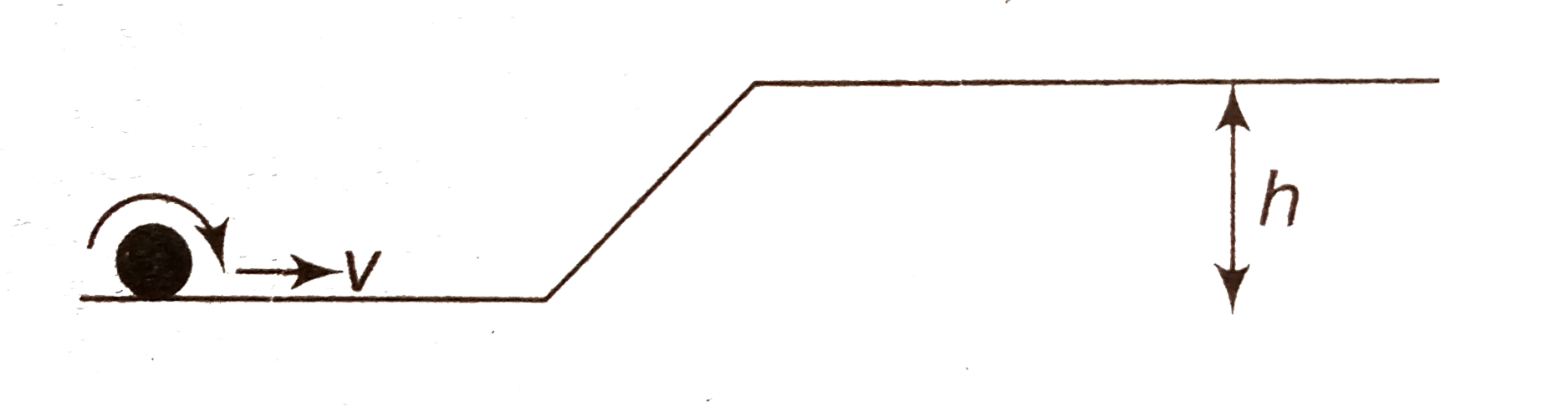 View Solution
View SolutionA small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration a0=g. The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is
 View Solution
View SolutionA solid sphere rolling on a rough horizontl surface with a lilner speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View SolutionA uniform solid sphere rolls on a horizontal surface with a linear speed of 10 m/s. It then rolls up a.plane inclined at 30° to horizontal. What is the height upto wlrich the sphere rises ? (See Fig.) Assume that the surface is frictionless. Also calculate the distance travelled by the Fig. sphere on the inclined plane ?
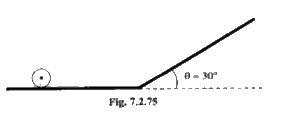 View Solution
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA sphere rolling on a horizontal rough surface collides elastically with a smooth vertical wall, as shown in figure. During collision, angular momentum of the sphere is conserved about ____________. (Any point O on the surface/point of contact P)
 View Solution
View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View Solution

