A table with smooth horiztonal surface is truning at an angular speed ω abouyt its axis. A groove is made on the surface along a radius and a particle is gently placed inside the groove at a distance a from the centre. Find the speed of the speed of the particle as its distance from teh centre becomes L.
v=ω2(L2−a2)13
v=ω(L2−a2)
v=ω2√L2−a2
v=ω√L2−a2
The correct Answer is:D
The situation is hwon in ure.
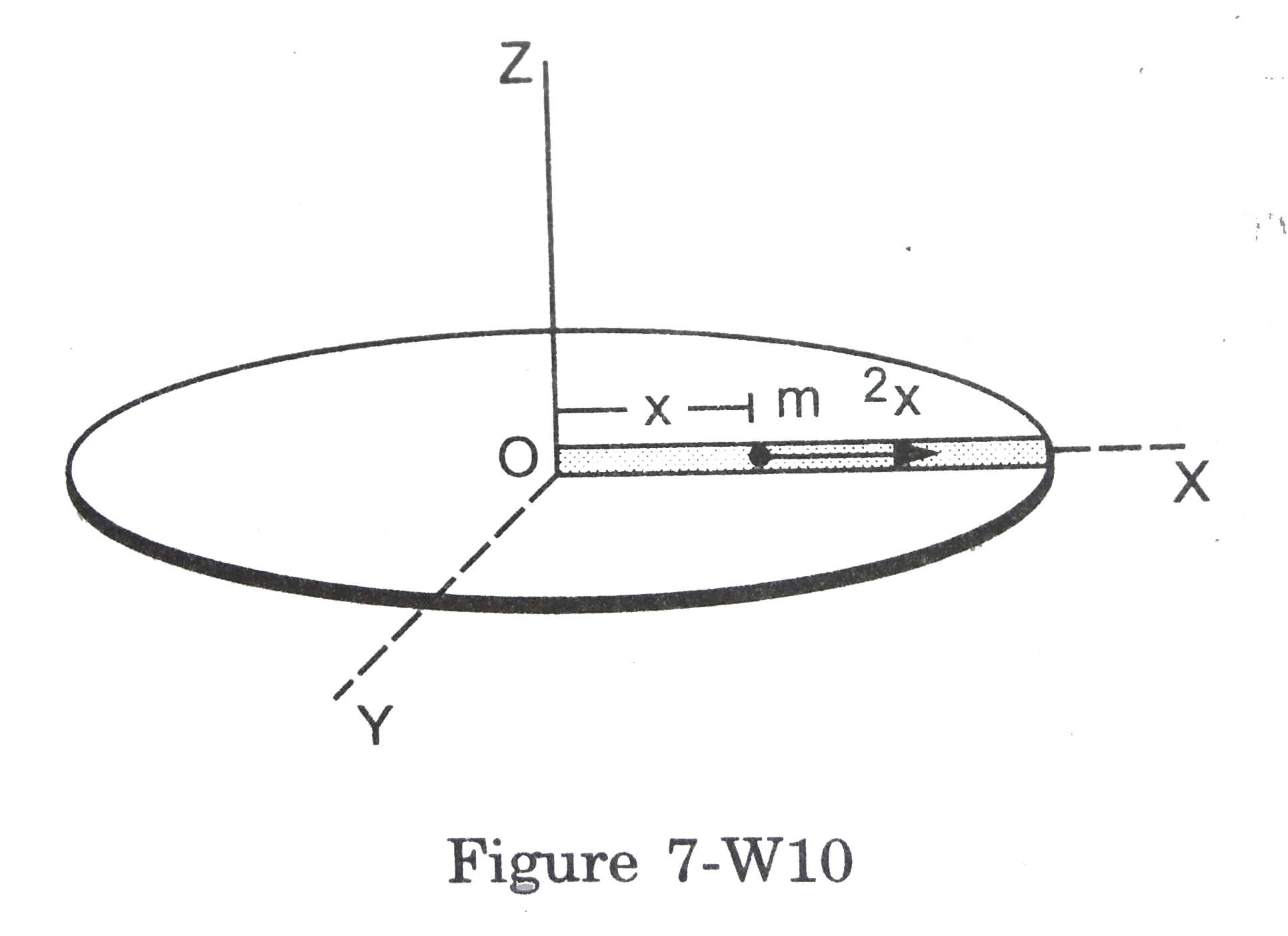
Let us work from the frame of reference of the table. Let us take the origin at the centre of rottion O an the X-axis along the groove ure. The Y-axis is along the lineperpendicular to OX coplaN/Ar with the surface of the table and the Z-axis is along the vertical.
Suppose at time t particle in the groove is at a distance x fromn the origin and is moving along The X-axis witha speed v. The forces acting on the particle (including the pseudeo forces that we must assume because we have taken our frame on the table which is rotating and is nonintertial) are
a. weight mg vetically downward
b. normal contact force N1 verticall upward by te bottom surfce of the groove,
c. normal contact force N2 parallel to the Y-axis by the side walls of the groove,
d. centrifugal force mω2x alongthe X-axis, and
e. Coriolis force along Y-axis (coriolis force is perpendicular to the velocity of the particle and the axis of rotation).
As the particle can only move in the groove. Its acceleration is along the X-axis. The only force along teh X-axis is the centrifugal force mω2x. all the other forces are perpendicular to the X-axis adn have no components along the X-axis.
Thus, the acceleration along the X-axis is
a=Fm=mω2xm=ω2x
or, dvdt=ω2x
or dvdx.dxdt=ω2x
or dvdx.v=ω2x
or, vdv=ω2xdx
or, ∫v_0vdv=∫L_aω2xdx
or, [12v2]v0=[12ω2x2]L_a
or, v22=12ω2(L2−a2)
or, v=omega sqrt(L^2-a^2)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Short Answer
10 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 1
15 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
_S01_013_Q01.png)
A very small groove is made in the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle fro that place.
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View Solution
Knowledge Check
If charge q is induced on outer surface of sphere of radius R, then intensity at a point P at a distance S from its centre is
Ainversely proportional to (S+R)2Binversely proportional to R2Cinversely proportional to S2Ddirectly proportional to S2A particle moving on the inside of a smooth sphere of radius r describing a horizontal circle at a distance r/2 below the centre of the sphere. What is its speed ?
A√5grB√4gr/3C√3gr/2D√√3grThe speed v of a particle moving along a straight line is given by a+bv2=x2 (where x is its distance from the origin). The acceleration of the particle is
AbxBx/aCx/bDx/ab
A tunnel is dug along a diameter of the earth. Find the force on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionEarth and moon centre distance is 'r'. From the mid point what should be the speed of the particle so that it can escape to infinity?
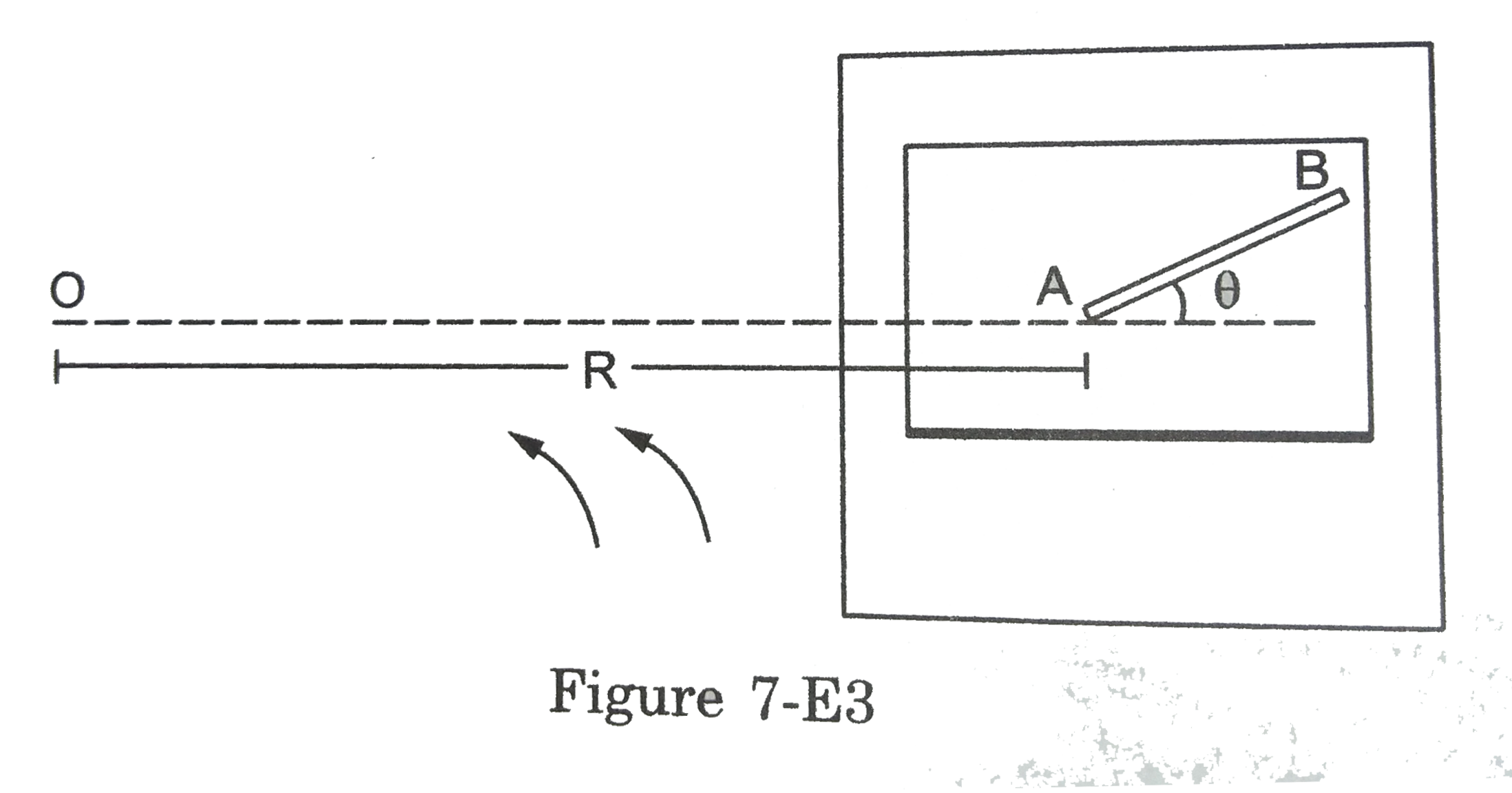
View SolutionA table with smooth horizontal surface is fixed in a cabin that rotates with a uniform angular velocity ω in a circular pathof radius R. A smooth groove AB of length L(<<R) is made on the surface of the table. The groove makes an angleθ with the radius OA of the circle in which the cabin rotates. A small particle is kept at the point A in the groove and is released to move along AB. Find the time taken by tehparticle to reach the point B.
View SolutionA particle is released from height S from the surface of the earth. At a certain height its KE is three times its PE. The height from the surface of earth and the speed of the particle at that instant are resp.
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2, where x is its distance from the origin. The acceleration of the particle is
View Solution
