A uniform rod AB of mass 3m and length 2l is lying at rest on a smooth horizontal table with a smooth vertical axis through the end A. A particle of mass 2m moves with speed 2u across the table and strikes the rod at its mid-point C if the impact is perfectly elastic. Find the speed of the particle after impact if
(a). It strikes rod normally,
(b). Its path before impact was inclinded at 60∘ to AC.
To solve the problem step by step, we will analyze both parts of the question systematically.
Given:
- Mass of the rod, mrod=3m
- Length of the rod, Lrod=2l
- Mass of the particle, mparticle=2m
- Initial speed of the particle, uinitial=2u
- The collision is perfectly elastic.
Part (a): Particle strikes the rod normally.
1. Identify the initial conditions:
- The rod is at rest, so its initial velocity vrod=0.
- The particle is moving with speed 2u towards the midpoint C of the rod.
2. Calculate the initial angular momentum:
- The distance from point A (the pivot) to point C is l.
- The initial angular momentum Linitial of the particle about point A is given by:
Linitial=mparticle⋅vinitial⋅r=2m⋅2u⋅l=4mul
3. Calculate the moment of inertia of the rod:
- The moment of inertia I of the rod about point A is:
I=13mrodL2rod=13(3m)(2l)2=13(3m)(4l2)=4ml2
4. Set up the conservation of angular momentum:
- After the collision, let the angular velocity of the rod be ω and the final velocity of the particle be v′.
- The final angular momentum Lfinal is:
Lfinal=I⋅ω+mparticle⋅v′⋅l=4ml2⋅ω+2m⋅v′⋅l
- Setting Linitial=Lfinal:
4mul=4ml2⋅ω+2m⋅v′⋅l
5. Use the conservation of kinetic energy:
- For a perfectly elastic collision:
12mparticle(vinitial)2=12mparticle(v′)2+12Iω2
- Substituting values:
12(2m)(2u)2=12(2m)(v′)2+12(4ml2)ω2
- This simplifies to:
4mu2=mv′2+4ml2ω2
6. Solve the equations:
- From the angular momentum equation:
4u=4lω+2v′
Rearranging gives:
v′=4u−4lω
- Substitute v′ into the kinetic energy equation and solve for v′.
7. Final result for part (a):
- After solving the equations, we find:
v′=2u3
Part (b): Particle strikes at an angle of 60∘ to AC.
1. Identify the components of the initial velocity:
- The component of the particle's velocity perpendicular to the rod (normal) is:
vnormal=2u⋅sin(60∘)=2u⋅√32=u√3
2. Use conservation of momentum:
- The initial momentum in the direction of the rod:
mparticle⋅vnormal=mparticle⋅v′+mrod⋅vrod
- Since the rod is initially at rest, we can simplify:
2m⋅u√3=2m⋅v′+0
3. Solve for v′:
- Rearranging gives:
v′=u√3
4. Final result for part (b):
- After substituting back into the equations and solving, we find:
v′=2u√33
Summary of Results:
- (a) Speed of the particle after impact when striking normally: v′=2u3
- (b) Speed of the particle after impact when striking at 60∘: v′=2u√33
- Mass of the rod, mrod=3m
- Length of the rod, Lrod=2l
- Mass of the particle, mparticle=2m
- Initial speed of the particle, uinitial=2u
- The collision is perfectly elastic.
- The rod is at rest, so its initial velocity vrod=0.
- The particle is moving with speed 2u towards the midpoint C of the rod.
- The distance from point A (the pivot) to point C is l.
- The initial angular momentum Linitial of the particle about point A is given by:
Linitial=mparticle⋅vinitial⋅r=2m⋅2u⋅l=4mul
- The moment of inertia I of the rod about point A is:
I=13mrodL2rod=13(3m)(2l)2=13(3m)(4l2)=4ml2
- After the collision, let the angular velocity of the rod be ω and the final velocity of the particle be v′.
- The final angular momentum Lfinal is:
Lfinal=I⋅ω+mparticle⋅v′⋅l=4ml2⋅ω+2m⋅v′⋅l
- Setting Linitial=Lfinal:
4mul=4ml2⋅ω+2m⋅v′⋅l
- For a perfectly elastic collision:
12mparticle(vinitial)2=12mparticle(v′)2+12Iω2
- Substituting values:
12(2m)(2u)2=12(2m)(v′)2+12(4ml2)ω2
- This simplifies to:
4mu2=mv′2+4ml2ω2
- From the angular momentum equation:
4u=4lω+2v′
Rearranging gives:
v′=4u−4lω
- Substitute v′ into the kinetic energy equation and solve for v′.
- After solving the equations, we find:
v′=2u3
- The component of the particle's velocity perpendicular to the rod (normal) is:
vnormal=2u⋅sin(60∘)=2u⋅√32=u√3
- The initial momentum in the direction of the rod:
mparticle⋅vnormal=mparticle⋅v′+mrod⋅vrod
- Since the rod is initially at rest, we can simplify:
2m⋅u√3=2m⋅v′+0
- Rearranging gives:
v′=u√3
- After substituting back into the equations and solving, we find:
v′=2u√33
- (a) Speed of the particle after impact when striking normally: v′=2u3
- (b) Speed of the particle after impact when striking at 60∘: v′=2u√33
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective30videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A rod of mass m and length l is lying on a horizontal table. Work done in making it stand on one end will be
View SolutionA uniform rod of mass m and length l is lying on a smooth table. An impulse J acts on the rod momentarily as shown in figure at point R. Just after that:
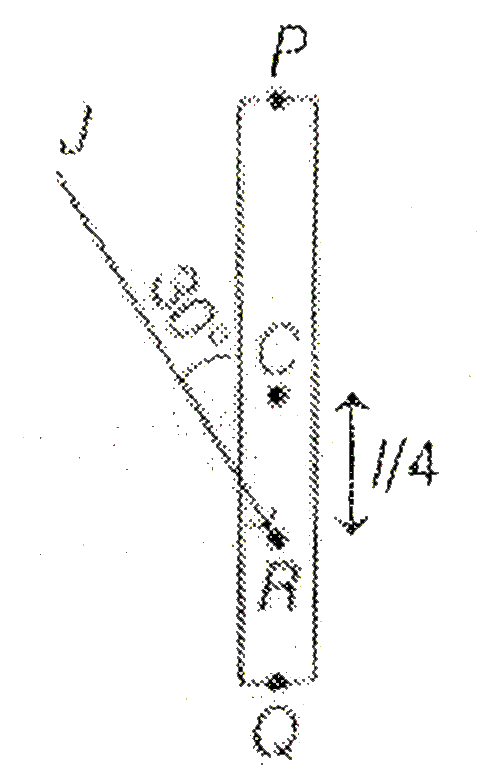
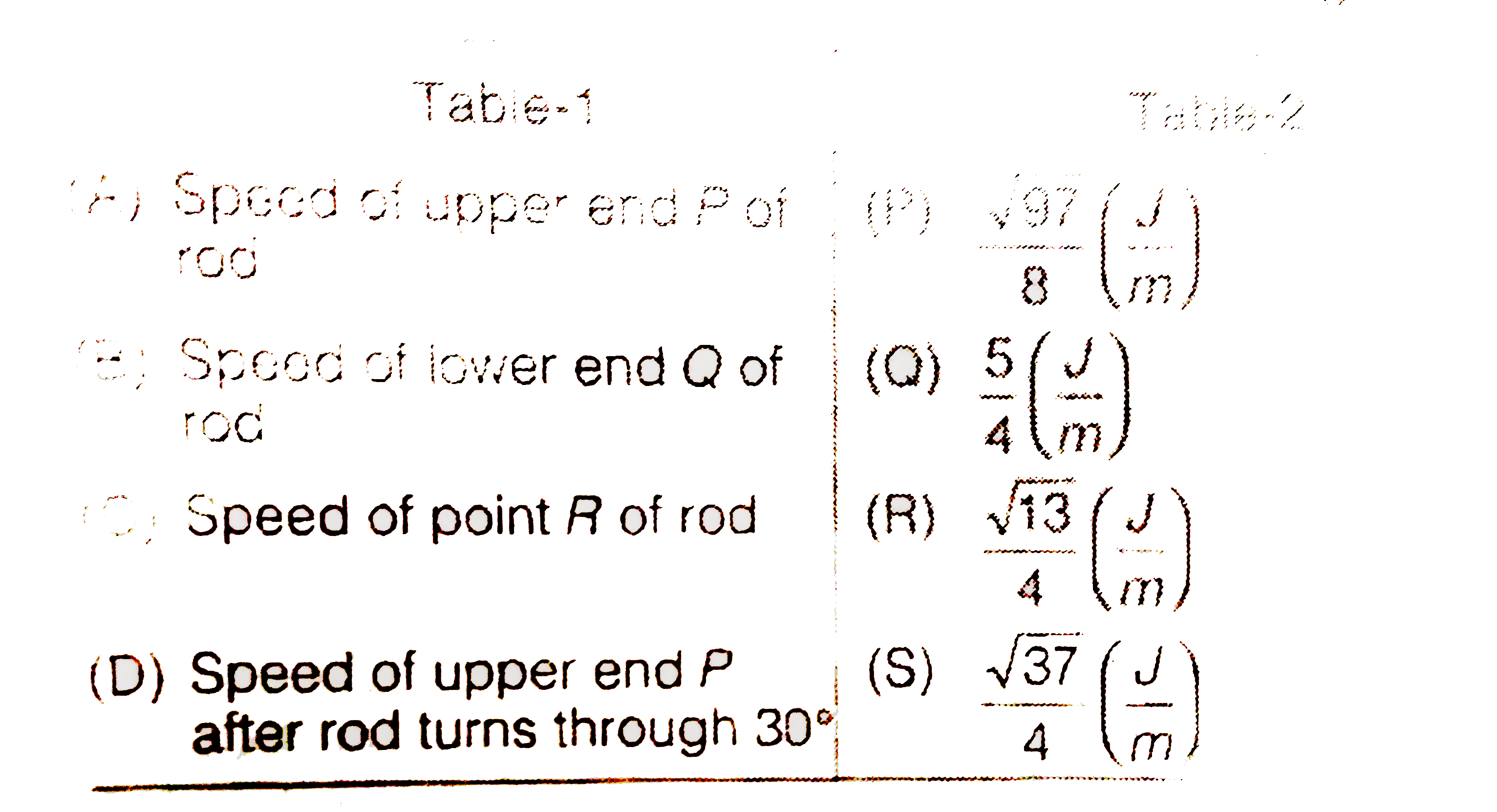 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :
 View Solution
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collisionView SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is
 View Solution
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of mass m and length L is kept on a horizontal table with L4 length on the table as shown in figure. As the string attached to the end B is cut, the angular acceleration of the rod about point C will be
_PHY_E05_242_Q01.png) View Solution
View SolutionA uniform rod of mass 2kg and length 1m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View Solution

