A wire carrying a current of 12A is in the form of a circle. It is necessary to have a magnetic field of induction 10−6 T at the centre. What should be the radius?
To find the radius of a circular wire carrying a current of 12 A that produces a magnetic field of induction 10−6 T at its center, we can use the formula for the magnetic field at the center of a circular loop:
B=μ0I2R
Where:
- B is the magnetic field induction (in Tesla),
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current (in Amperes),
- R is the radius of the circular loop (in meters).
1. Identify the known values:
- Current, I=12A
- Magnetic field, B=10−6T
- Permeability of free space, μ0=4π×10−7T m/A
2. Substitute the known values into the formula:
10−6=(4π×10−7)×122R
3. Rearrange the equation to solve for R:
2R×10−6=(4π×10−7)×12
R=(4π×10−7)×122×10−6
4. Calculate the right side:
R=(4×3.14×10−7)×122×10−6
R=(1.256×10−6)×122×10−6
R=1.5072×10−52×10−6
R=7.536m
5. Final result:
The radius R of the circular wire should be approximately 7.54m.
Summary:
Thus, the radius of the circular coil should be 7.54m to achieve a magnetic field of 10−6T at the center.
- B is the magnetic field induction (in Tesla),
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current (in Amperes),
- R is the radius of the circular loop (in meters).
- Current, I=12A
- Magnetic field, B=10−6T
- Permeability of free space, μ0=4π×10−7T m/A
10−6=(4π×10−7)×122R
2R×10−6=(4π×10−7)×12
R=(4π×10−7)×122×10−6
R=(4×3.14×10−7)×122×10−6
R=(1.256×10−6)×122×10−6
R=1.5072×10−52×10−6
R=7.536m
The radius R of the circular wire should be approximately 7.54m.
Thus, the radius of the circular coil should be 7.54m to achieve a magnetic field of 10−6T at the center.
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -II)
40 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - EXERCISE (VERY SHORT ANSWER QUESTIONS )
19 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A wire of length 2 m carrying a current of 1 A is bend to form a circle. The magnetic moment of the coil is (in Am2)
View SolutionA wire carrying a current i is first bent in the form of a square of side a and placed at right angle to a uniform magnetic field of induction B. The work done in changing its shape' into a circle is
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA straight wire carrying a current of 13 A is bent into a semi-circular arc of radius 2 cm as shown in figure. The magnetic field is 1.5×10−4T at the centre of arc, then the magnetic field due to straight segment is

View SolutionA long straight wire carrying current of 30A is placed in an external uniform magnetic field of induction 4×10−4T. The magnetic field is acting parallel to the direction of current. The magnitude of the resultant magnetic induction in tesla at a point 2.0cm away from the wire is
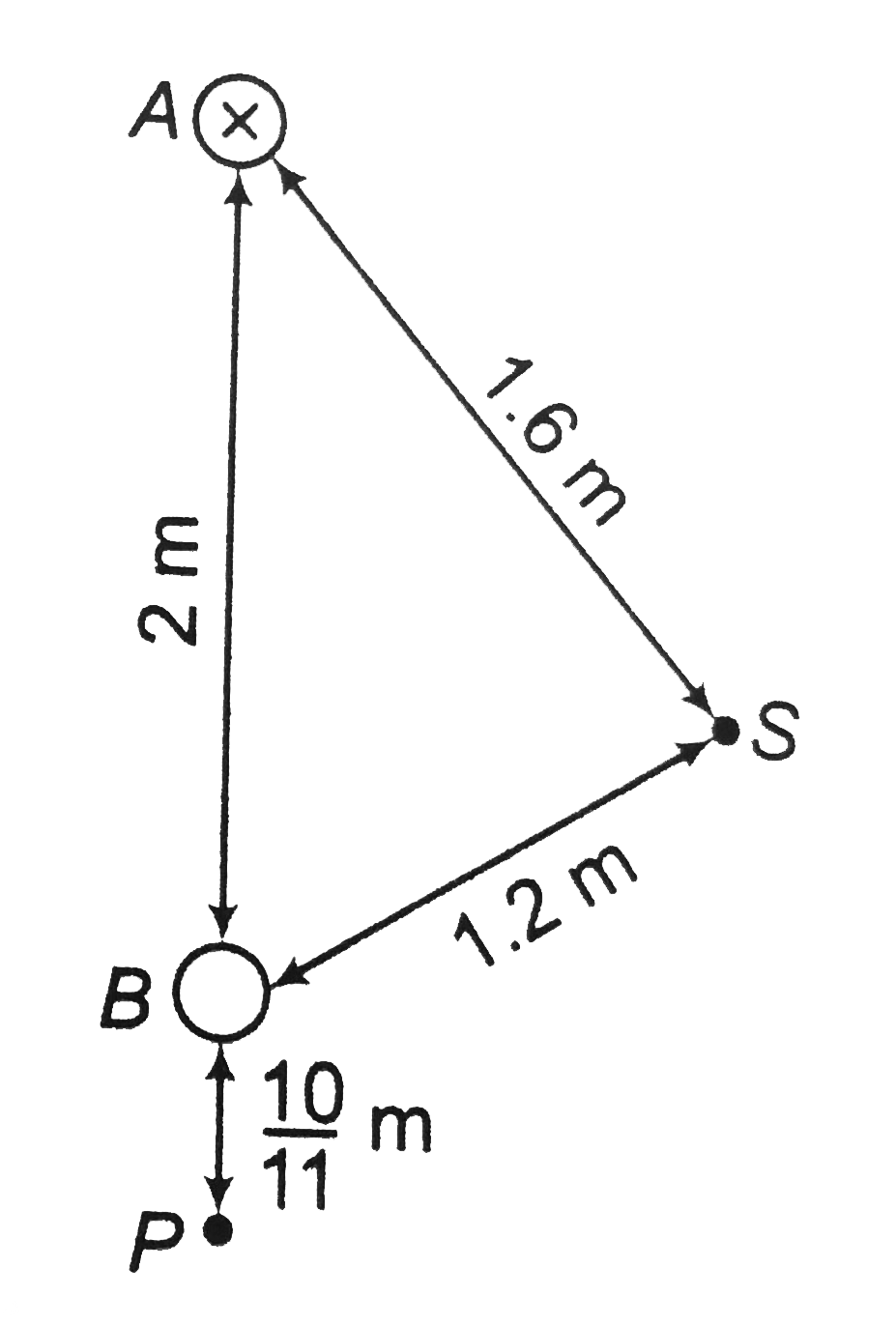
View SolutionTwo long straight parallel wieres are 2m apart, perpendicular to the plane of the paper. The wire A carries a current of 9.6A, directed into the plane of the paper. The wire B carries a current such that the magnetic field of induction at the point P, at a distance of 1011 m from the wire B, is zero. find
a. the magnitude and directiion of the current in B.
b. the magnitude of the magnetic field of induction of the pont S.
c. the force per unit length on the wire B.
View SolutionA long straight wire carrying current of 30A is placed in an external unifrom magnetic field of induction 4×104T. The magnetic field is acting parallel to the direction of current. The maggnetic of the resultant magnetic inuduction in tesla at a point 2.0cm away form the wire is
View SolutionIn a wire of circular form has 4A current is following to have a magnetic induction as 1μT , at its centre. The radius of circle should be approximately
View SolutionA wire of length l meter carrying current i ampere is bent in form of circle. Magnetic moment is
View SolutionA long cylindrical wire carrying current of 10A has radius of 5mm find its its magnetic field induction at a point 2mm from the centre of the wire
View Solution
