An electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
To solve the problem of calculating the electric potential at point P due to an electric dipole, we will follow these steps:
Given:
- An electric dipole consists of charges +q and −q separated by a distance 2a.
- The dipole is aligned along the X-axis and centered at the origin.
(i) Calculate the electric potential at point P
1. Identify the positions of the charges:
- The positive charge +q is located at x=a.
- The negative charge −q is located at x=−a.
2. Determine the distance from point P to each charge:
- Let the distance from point P (located at x=d) to the positive charge +q be r1=d−a.
- The distance from point P to the negative charge −q is r2=d+a.
3. Write the expression for the electric potential due to each charge:
- The electric potential V1 due to the positive charge +q is given by:
V1=kqr1=kqd−a
- The electric potential V2 due to the negative charge −q is given by:
V2=−kqr2=−kqd+a
4. Calculate the total electric potential at point P:
- The total electric potential V at point P is the sum of the potentials due to both charges:
V=V1+V2=kqd−a−kqd+a
5. Combine the fractions:
- To combine the fractions, we find a common denominator:
V=kq((d+a)−(d−a)(d−a)(d+a))=kq(2a(d−a)(d+a))
- Therefore, the electric potential at point P is:
V=2akq(d−a)(d+a)
(ii) Calculate V at a point far from the dipole
1. Consider the case when point P is far from the dipole:
- When d is much larger than a (i.e., d≫a), we can approximate:
V≈2akqd2
2. Relate the dipole moment p:
- The dipole moment p is defined as:
p=q⋅(2a)
- Thus, we can express V in terms of the dipole moment:
V≈pd2
Final Results:
- The electric potential at point P is:
V=2akq(d−a)(d+a)
- At a point far from the dipole:
V≈pd2
- An electric dipole consists of charges +q and −q separated by a distance 2a.
- The dipole is aligned along the X-axis and centered at the origin.
- The positive charge +q is located at x=a.
- The negative charge −q is located at x=−a.
- Let the distance from point P (located at x=d) to the positive charge +q be r1=d−a.
- The distance from point P to the negative charge −q is r2=d+a.
- The electric potential V1 due to the positive charge +q is given by:
V1=kqr1=kqd−a
- The electric potential V2 due to the negative charge −q is given by:
V2=−kqr2=−kqd+a
- The total electric potential V at point P is the sum of the potentials due to both charges:
V=V1+V2=kqd−a−kqd+a
- To combine the fractions, we find a common denominator:
V=kq((d+a)−(d−a)(d−a)(d+a))=kq(2a(d−a)(d+a))
- Therefore, the electric potential at point P is:
V=2akq(d−a)(d+a)
- When d is much larger than a (i.e., d≫a), we can approximate:
V≈2akqd2
- The dipole moment p is defined as:
p=q⋅(2a)
- Thus, we can express V in terms of the dipole moment:
V≈pd2
- The electric potential at point P is:
V=2akq(d−a)(d+a)
- At a point far from the dipole:
V≈pd2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.1
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.2
15 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
An electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
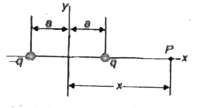
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionAn electric dipole consists of two opposite charges each of magnitude 2 μC separated by a distance 1 cm. The dipole is placed in an external field of 103 N/C. The maximum torque on the dipole is
View SolutionAn electric dipole consists of two opposite charges of magnitude 1μC separated by a distance of 2cm.The dipole is placed in an electric filled 10−5Vm−1.The maximum torque that the field exert on the dipole is
View SolutionAn electric dipole consists of two opposite charges of magnitude 1/3×10−7C, separated by 2 cm. The dipole is placed in an external field of 3×107NC−1. What maximum torque does the electrc field exert on the dipole ?
View SolutionDerive the expression for the electric potential at any point along the axial line of an electric dipole.
View SolutionWe have two electric dipoles. Each dipole consists of two equal and opposite point charges at the ends of an insulating rod of length d. The dipoles sit along the x-axis a distance r aparts oriented as shown in fig. Their separation rgtgtd. The dipole on the left:

View SolutionA charge +Q is fixed at the origin of the co-ordinate system while a small electric dipole of dipolement →p pointing away from the charge along the x-axis is set free from a point far away from the origin.
(a) Calculate the K.E. of the dipole when it reaches to a point (d, 0).
(b) Calculate the force on the charge +Q at this moment.
View SolutionAn electric dipole consisting of two opposite charges of 2×10−6C each separated by a distance of 3cm is placed in an electirc field of 2×105N/C. The maximum torque on the dipole is will be
View SolutionAn electric dipole is formed by +4μC and −4μCcharges at 5 m m distance. Calculate the dipole moment and give its direction.
View Solution
