An ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
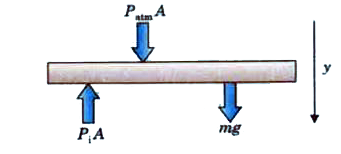
Let the area of cross section of the piston and the cylinder be A. Forces acting on the piston at equilibrium are
PatmA+mg=P1A …(i)

When the piston is down by a distance y, restoring force on it is
⇒F=PatmA+mg−(P1+dp)A
=P1A−(Pi+dP)A=−AdP
For an adiabatic process, PV = constant
Differentiating partially, we get
⇒PγVγ−1dV+VγdP+0
⇒dP=γPdVV=−γPiVi.Ay
F=−AdP⇒ F=−γPiA2Viy=−ky
Frequency, f=12π√km=12π√γPiA2mVi
Topper's Solved these Questions
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT FILE (Textbook Exercises)
19 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - NCERT (Additional Exercises)
6 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Conceptual Questions
18 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
Similar Questions
Which of the following examples represent periodic motion?
(a) A swimmer completing one return trip from one bank of a river to other bank. (b) A freely suspended bar magnet displaced from its N−S direction and released. (c) A hydrogen molecule rotating about its centre of mass. (d) An arrow released from a bow.
View SolutionAn air chamber of volume v has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction. Show that when the ball is pressed down a little and released for the time priod of oscillation, assuming pressure-volume variations of the air to be isothermal.
View SolutionIf acceleration ∝ displacement, will that be a sufficient condition for simple harmonic motion ?
View SolutionWhen can say that circular motion is periodic ?
View SolutionWhat are the main features of gravitational force?
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionA smooth piston of mass m area of cross - section A is in equilibrium in a gas jar when the pressure of the gas is P_(0) . Find the angular frequency of oscillation of the piston, assuming adiabatic Change of state of the gas.
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volum of the gas is V0 and its pressur is P0. The pistong is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionIn a cylinder filled up with ideal gas end gas and closed from both ends there is a piston of mass m and cross − sectional area S (figure).In equilibrium the piston divides the cylinder into two equal parts, each with volime V0 . The gas ppressure is p0. The piston was slightly displaced from the equlibrium position and released.Find the oscillation frequency, assuming the prosecces in the gas to be adiabatic and the friction negligible.
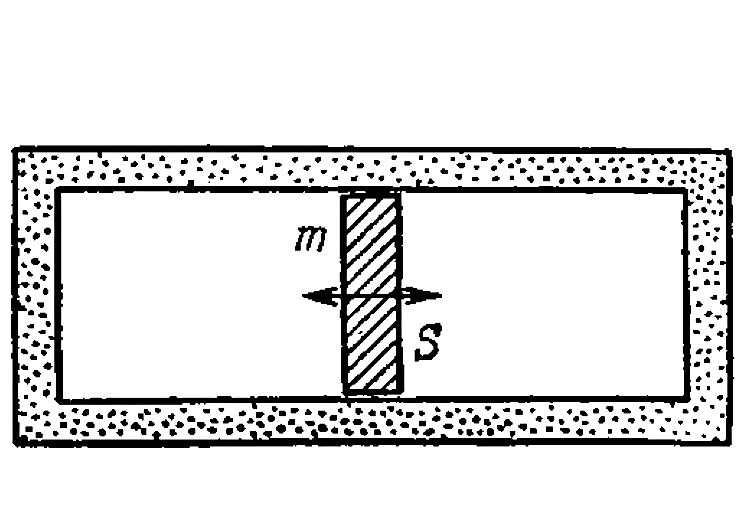
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V_(0) and pressure P_(0) in equilibrium Assume the sepatator to move without friction. If the piston is slightly displaced by x, the net force acting on the piston is
View SolutionA closed and isolated cylinder contains ideal gas. An adiabatic separator of mass m, cross sectional area A divides the cylinder into two equal parts each with volume V0 and pressure P0 in equilibrium Assume the sepatator to move without friction.
The time period of oscillation for small displacements of the piston is
View Solutionएक आदर्श गैस ऊध्वार्धर बेलनाकार बर्तन में भरी है जो M द्रव्यमान की मुक्त रूप से गतिमान एक पिस्टन से बन्द है। पिस्टन तथा बेलन का अनुप्रस्थ परिच्छेद-क्षेत्रफल A है। जब पिस्टन सन्तुलन में ही, गैस का आयतन V0 तथा दाब P0 है। पिस्टन को सन्तुलन स्थिति से थोड़ा विस्थापित करके छोड़ दिया जाता है। यह मानकर कि निकाय परिवेश से पूर्णतया विलगित है, पिस्टन सरल आवर्त्त गति करती है, जिसकी आवृति है :
View Solutionएक ऊर्ध्वाधर बेलनाकार बर्तन में भरी आदर्श गैस स्वतंत्रतापूर्वक चलायमान द्रव्यमान M के पिस्टन को साधे हुए है | पिस्टन तथा बर्तन दोनों का अनुप्रस्थ क्षेत्रफल A है | संतुलन की स्थिति में गैस का आयतन V0 तथा दाब P0 है | संतुलन की स्थिति से पिस्टन को थोड़ा - सा विस्थापित करके छोड़ा जाता है | यदि निकाय, वातावरण से पूर्णत : विलग है तो पिस्टन के सरल आवर्ती दोलनों की आवृत्ति होगी :
View SolutionAn ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
View SolutionAn ideal gas enclosed in a vertical cylindrical container supports a freely moving pistion of mass M. The pistion and the cylinder have equal cross sectional area A. When the pistion is in equilibrium, the volume of the gas is V0 and its pressure is P0. The pistion is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the pistion executes a simple harmonic motion with frequency
View SolutionAn ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass M. The piston and cylinder have equal cross sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the quilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency :
View Solution
