An inductance L and a resistance R are first connected to a battery. After some time the battery is disconnected but L and R remain connected in a closed circuit. Then the current reduces to 37% of its initial value in
RL second
RLsecond
LRsecond
1LRsecond
The correct Answer is:C
To solve the problem, we need to analyze the behavior of the current in an RL circuit when the battery is disconnected. The current in the circuit decreases over time due to the inductor's property of opposing changes in current.
1. Understanding the Circuit: Initially, we have an inductor (L) and a resistor (R) connected to a battery. When the battery is connected, the current increases until it reaches a maximum value (I₀) determined by the battery voltage and the resistance.
2. Current Growth Equation: The current growth in the circuit when the battery is connected can be described by the equation:
I(t)=I0(1−e−t/τ)
where τ=LR is the time constant of the circuit.
3. Battery Disconnection: After some time, the battery is disconnected. The inductor will now oppose the change in current, and the current will start to decay.
4. Current Decay Equation: The current decay in the circuit after the battery is disconnected is given by:
I(t)=I0e−t/τ
5. Finding Time for 37% Current: We need to find the time t when the current reduces to 37% of its initial value I0. This means:
I(t)=0.37I0
Substituting this into the decay equation:
0.37I0=I0e−t/τ
6. Simplifying the Equation: We can divide both sides by I0 (assuming I0≠0):
0.37=e−t/τ
7. Taking Natural Logarithm: Taking the natural logarithm of both sides gives:
ln(0.37)=−tτ
8. Solving for Time t: Rearranging the equation to solve for t:
t=−τln(0.37)
9. Substituting τ: Recall that τ=LR, so we can substitute this into our equation:
t=−LRln(0.37)
10. Final Expression: Thus, the time taken for the current to reduce to 37% of its initial value is:
t=LRln(10.37)
I(t)=I0(1−e−t/τ)
where τ=LR is the time constant of the circuit.
I(t)=I0e−t/τ
I(t)=0.37I0
Substituting this into the decay equation:
0.37I0=I0e−t/τ
0.37=e−t/τ
ln(0.37)=−tτ
t=−τln(0.37)
t=−LRln(0.37)
t=LRln(10.37)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
An inducatane L and a resistance R are connected in series with a battery of emf epsilon. Find the maximum rate at which the energy is stored in the magnetic field.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA Capacitor C and resister R are connected to a battery of 5V in series. Now battery is disconnected and a diode is connected as shown in figure (a) and (b) respectively. Then charge on the capacitor after time RC in (a) and (b) respectively is QA and QB. Their value are
 View Solution
View SolutionA coil of resistance 40Ω is connected across a 4.0 V battery. 0.10 s after the battery is connected, the current in the coil is 63 mA. Find the inductance of the coil.
View SolutionAn inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View SolutionA coil of self inductance 10 mH and resistance 0.1 Ω is connected through a switch battery of internal resistance 0.9Ω after the switch is closed, the time taken for the current to attain 80% of the saturation value is [taken ln5=1.6]
View SolutionAn indcutor having self inductance L with its coil resistance R is connected across a battery of emf elipson. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL (ngt1).
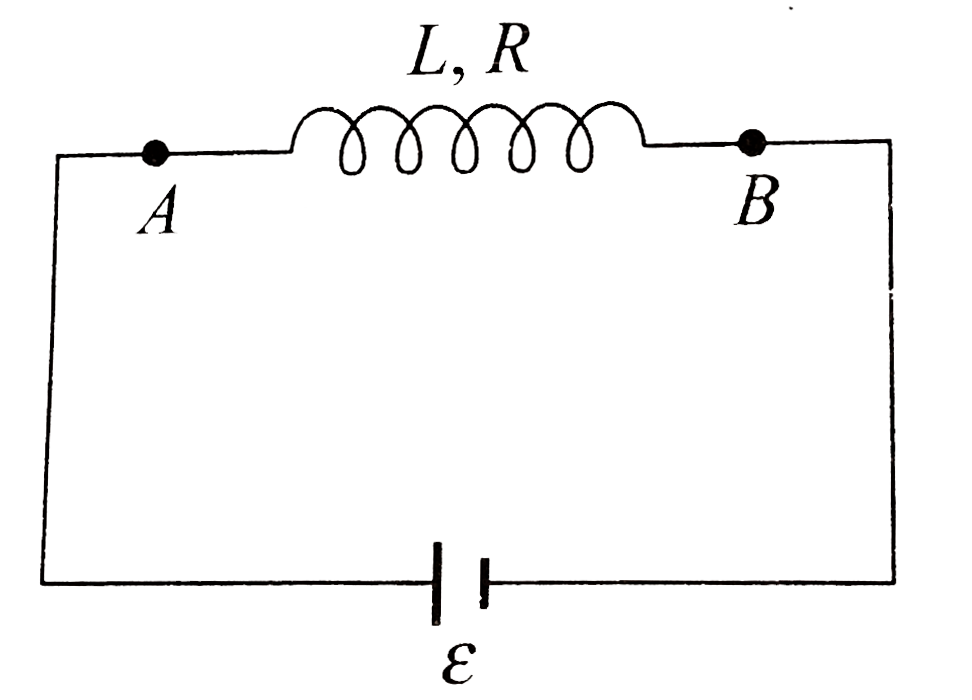
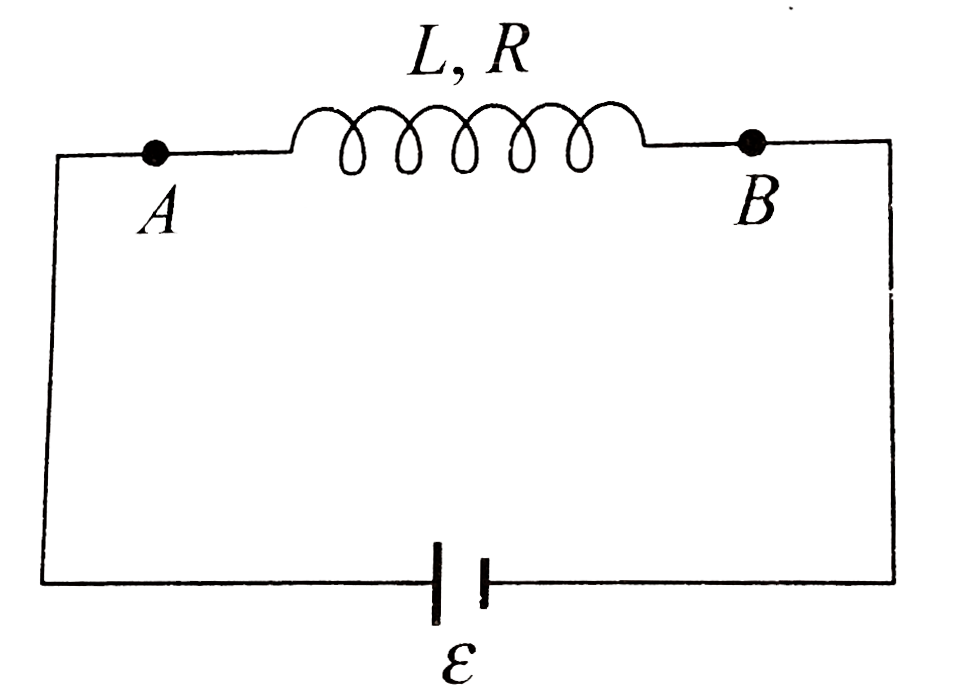
after insertion of rod, current in the circuit:View SolutionAn inductor having self inductance L with its coil resistance R is connected across a battery of emf ε. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL(n>1).
When again circuit is in steady state, the current in it isView SolutionA coil of inductance L=50μH and resistance = 0.5Ω is connected to a battery of emf = 5V.
A resistance of 10Ω is connected parallel to the coil. Now, at the same instant the connection of the battery is switched off. Then, the amount of heat generated in the coil after switching off the battery isView SolutionFive equal resistances each of resistance R are connected as shown in the figure. A battery of V volts is connected between A and B. The current flowing in AFCEB will be
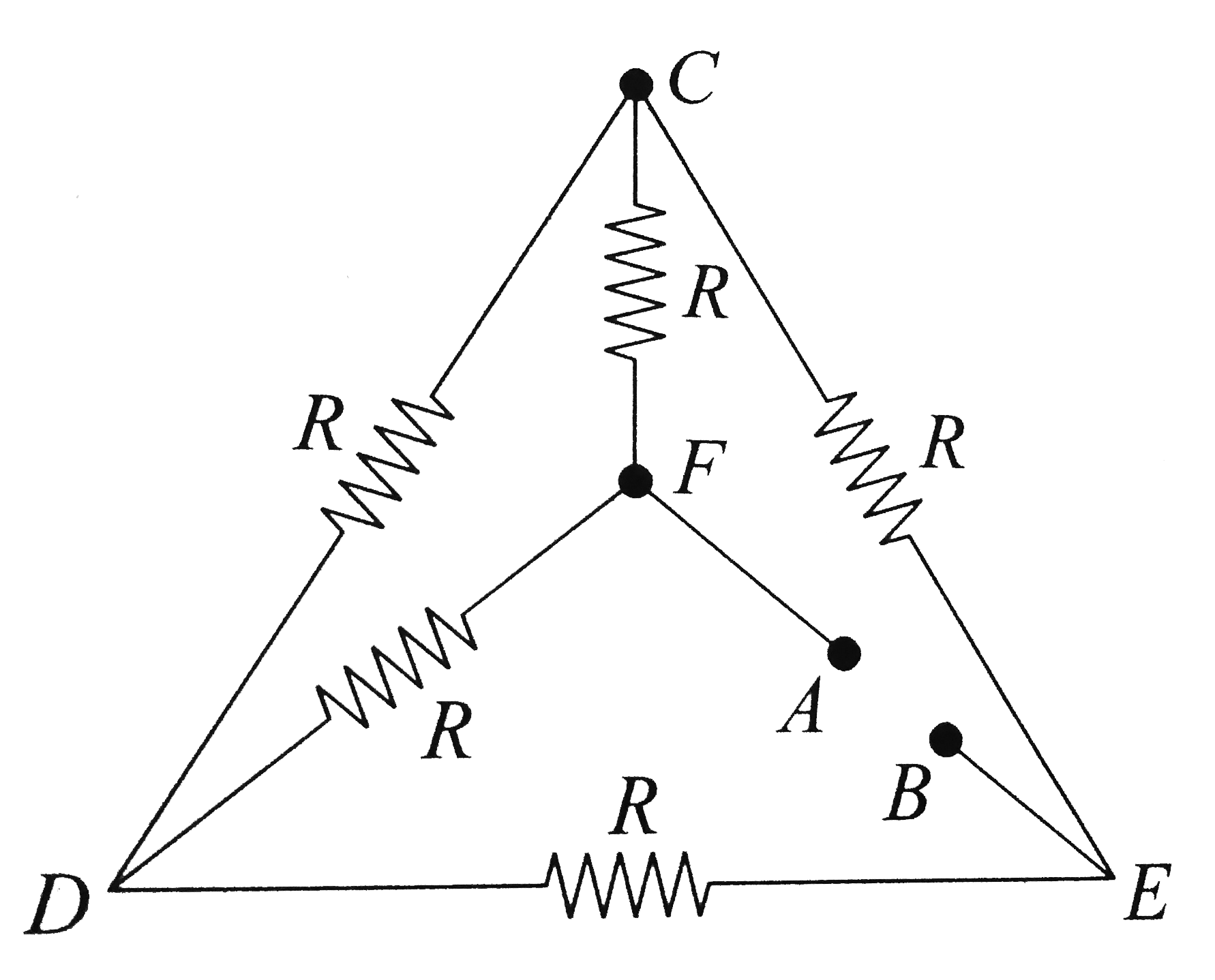 View Solution
View Solution

