Find the electric field at a point P on the perpendicular bisector of a uniformly charged rod. The lengthof the rod is L, the charge on it is Q and the distance of P from the centre of the rod is a.Solution in Tamil

Let us take an element of length dx at a distance x from
the centre of the rod . The charge on this
element is
dQ=QLdx.
The electric field at P due to this element is
dE=dQ4πε0(AP)2
. By symmetry, the resultant field at P will be along OP
(if the charge is positive). The component of dE along
OP is
dEcosθ=dQ4πε0(AP)2.OPAP=aQdx4πesilon0L(a2+x2)32
Thus, the resultant field at P is
E=∫dEcosθ
=aQ4πesilon0L∫L2−L2dxa2+x2(32).
We have x=atanθordx=asec2θdthη.
theus,∫dx(a2+x2)32=∫αsec2θdthηθalpah3sec3θ<br>= (1)/(a^2) int cos theta d theta = (1)/(a^2) sin theta = (1)/(alpha^2) (x)/(x^2 + alpha^2 )^(1/2)<br>.From(i)<br>E=(alphaQ)/(4piepsilon_0 La^2) [(x)/(x^2 + alpha^2 )^(1/2) ]_(-L/2)^(L/2)<br>= (aQ)/(4piepsilon_0 La^2) [(2L)/(L^2+4alpah^2)^(1/2)]<br>= (Q)/(2piepsilon_0 alpha sqrt(L^2+4a^2)).
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 1
9 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercise
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
98 Videos
Similar Questions
The charge on a proton is +1.6X10(−19)C and that on an
. electron is −1.6X10(−19)C. Does it mean that the electron
. has a charge 3.2X10(−19)c less than the charge of a
. proton?
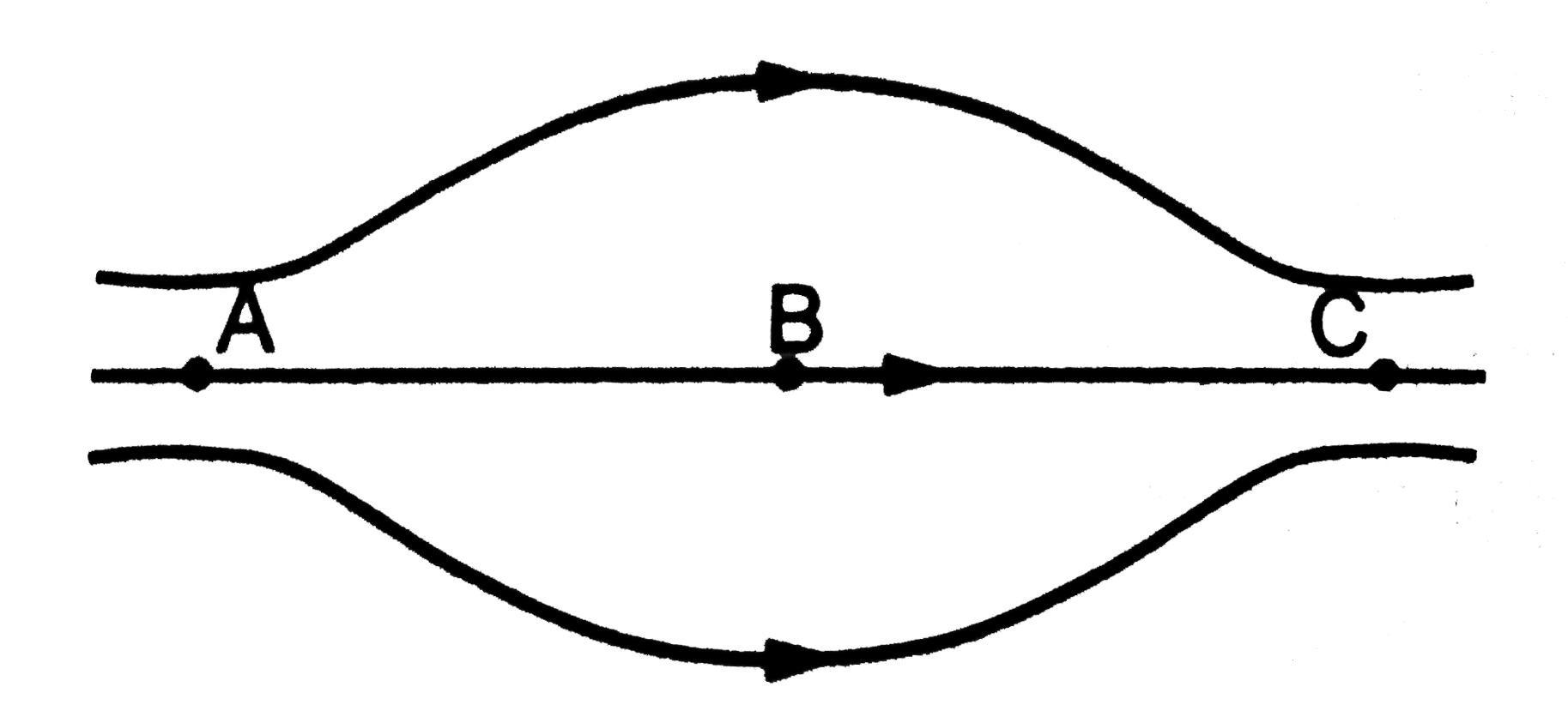
View SolutionFigure shows some of the electric field lines correspoinding to an electric field. The figure suggests that
View SolutionFind the dimensional formula of ε0 .
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
View SolutionCalculate the dimensions of (a) ∫→E.d→l,(b)vBlanddΦ0dt. The symbols have their usual meanings.
View SolutionA rod of length l, has a uniform positive charge per unit length and a total charge Q. calculate the electric foeld at a point P located along the long axis of the rod and at a distance a from one end

View SolutionCalculate the potential at a point on the perpendicular bisector of uniformly charged thin rod (linear density of charge =λ) of length 2l at a distance a from the centre of the rod.
View SolutionA rod length l is uniformly charged with charge q. Calculate potential at point P.
View Solutionएकसमान आवेशित छड़ जिसकी लम्बाई 2l तथा कुल आवेश q है, के कारण उसके लम्ब समद्विभाजक पर दूरी r पर स्थित किसी बिन्दु पर विद्युत् क्षेत्र की तीव्रता ज्ञात कीजिए।
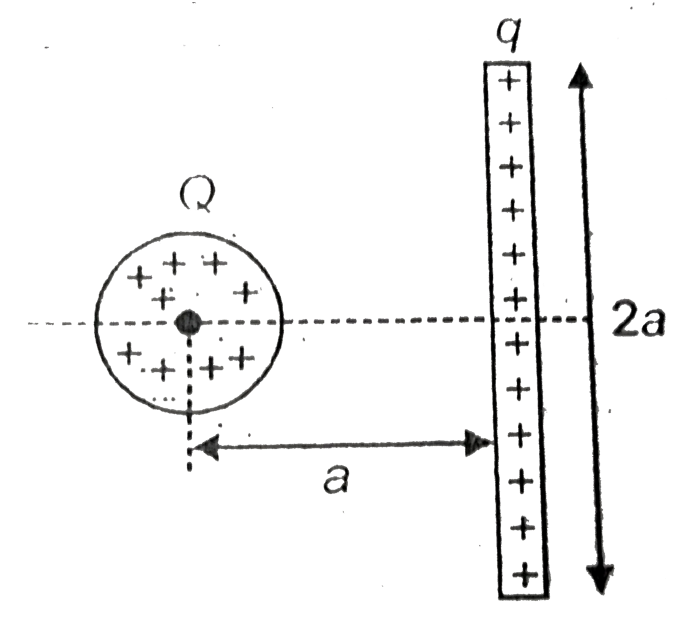
View SolutionA uniformly charged sphere, made up of non-conducting material and carrying charge Q, is placed near a uniformly charged non-conducting rod, carrying charge q. The centre of the sphere lies on the perpendicular bisector of the rod as shown in the figure. Calculate the force exerted by the sphere on the rod.
View SolutionFind the electric field and potential at the centre of curvature of a uniformly charged semicircular rod of radius R with a total charge Q in SI. lambda is the linear charge density.
View SolutionThe electric field at a point P which is at a distance l on the perpendicular bisector of a uniformly charged wire of length 1 , charge Q=Q2πɛ0l2√k where k = ?
View SolutionCalculate electric field intensity at point P due to a thin positive uniformly charged rod . Point P is at perpendicular distance d from the rod . The lower and upper ends of the rod make the angles α and β as shown below .
View SolutionFind : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.
View SolutionFigure 22-24 shows a plastic rod having a uniformly distributed charge. The charge per unit length of the rod is lambda . Find the electric field due to the rod at a point P which is at a distance r from the rod.
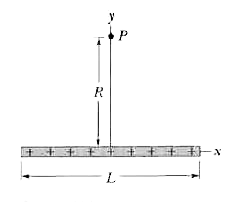
View SolutionIn Fig., positive charge q = 9.25 pC is spread uniformly along a thin nonconducting rod of length L = 16.0 cm. What are the (a) magnitude and (b) direction (relative to the positive direction of the x axis) of the electric field produced at point P, at distance R = 6.00 cm from the rod along its perpendicular bisector ?
View Solution
