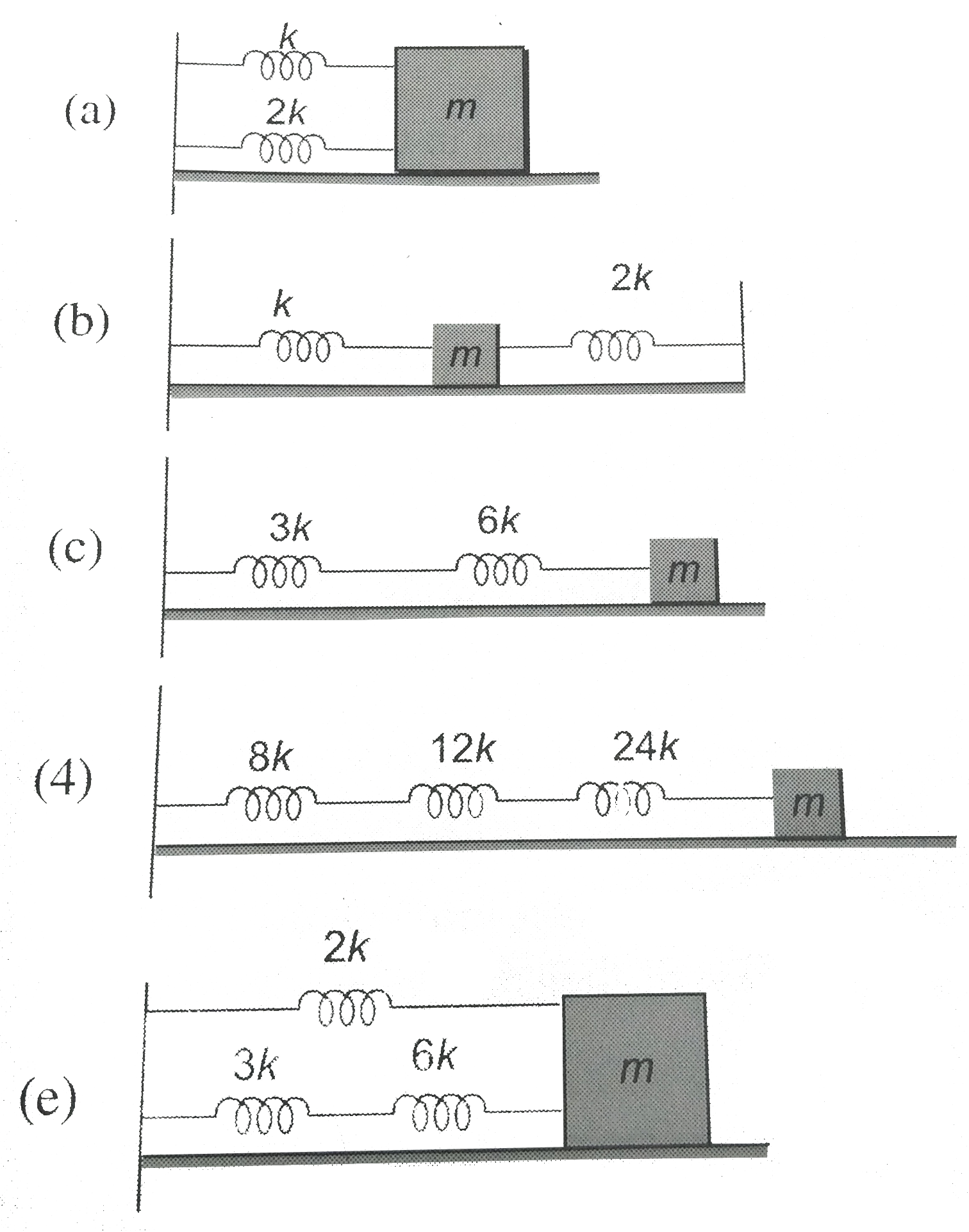
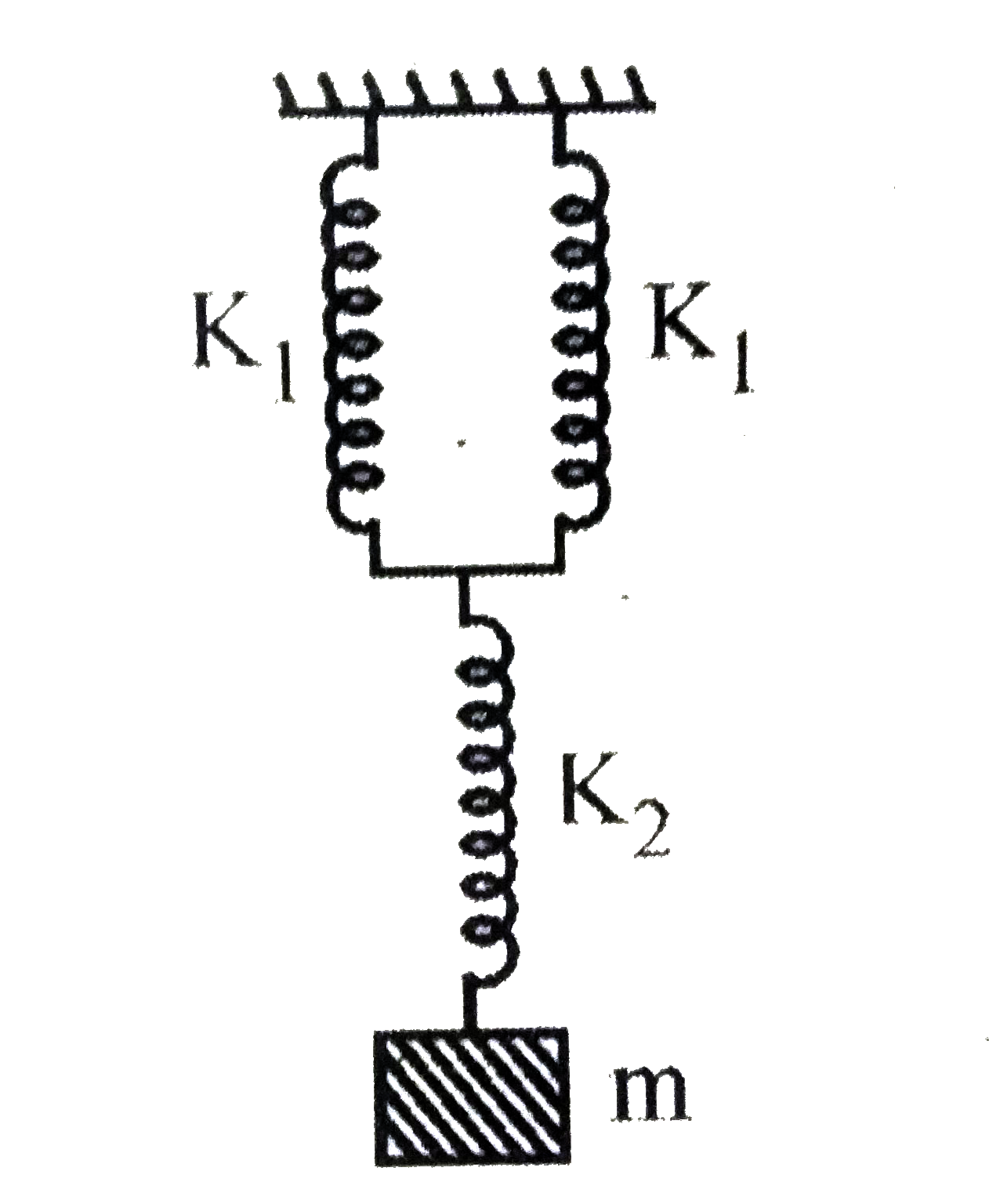
Find the time period of the oscillation of mass m in figure a,b,c what is the equivalent spring constant of the pair oif springs in each case?
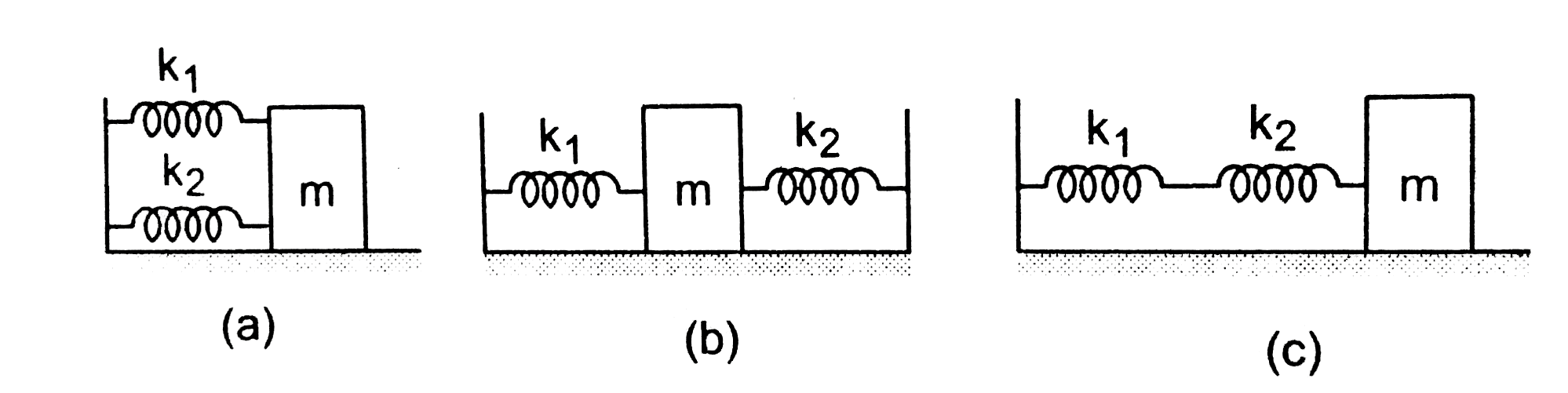
The correct Answer is:=2π√mk1+k2
=2π(√m(k1+k2)k1k2)
a. Equivalent spring constant
=k=k1+k2(parallel)
T=2π√mk=2π√mk1+k2
b. Let us displace theh block m towards left through dislacement x.
Resultant force F=F1+F2=(k1+k2)
Acceleration
(Fm)=(k1+k2)mx
Timeperiod
=T=2π√displacementAe≤ration
→2π√xx(k1+k2m)
=2π√mk1+k2
The equivalent spring constant
k=k1+k2 . c In series connectionn equivalent spring constant be k
So,k 1k=1k1+1k2=k2+k1k1k2
→K=k1k2k1+k2
T=2√mk
=2π(√m(k1+k2)k1k2)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
Knowledge Check
Find the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
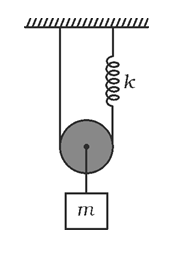 A2π√mkBπ√mkC4π√mkD2π√m2k
A2π√mkBπ√mkC4π√mkD2π√m2kWhat is the mechanical equivalent of spring constant k in LC oscillating circuit?
A1LB1CCLCD1LCCalculate the period of oscillations of block of mass m attached with a set of springs as shown
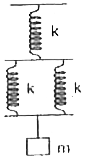 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
What will be the equivalent spring constant of the spring system shown in the figure ?
View SolutionWhat is the mechanical equivalent of spring constant K, in I.C oscillating circuit ?
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
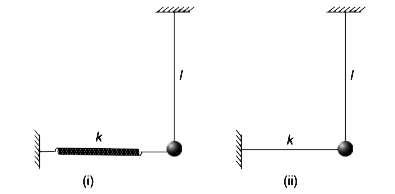
View SolutionA simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View SolutionThe time period of an oscillating spring of mass 630 g and spring constant 100 N/m with a load of 1 kg is
View Solution