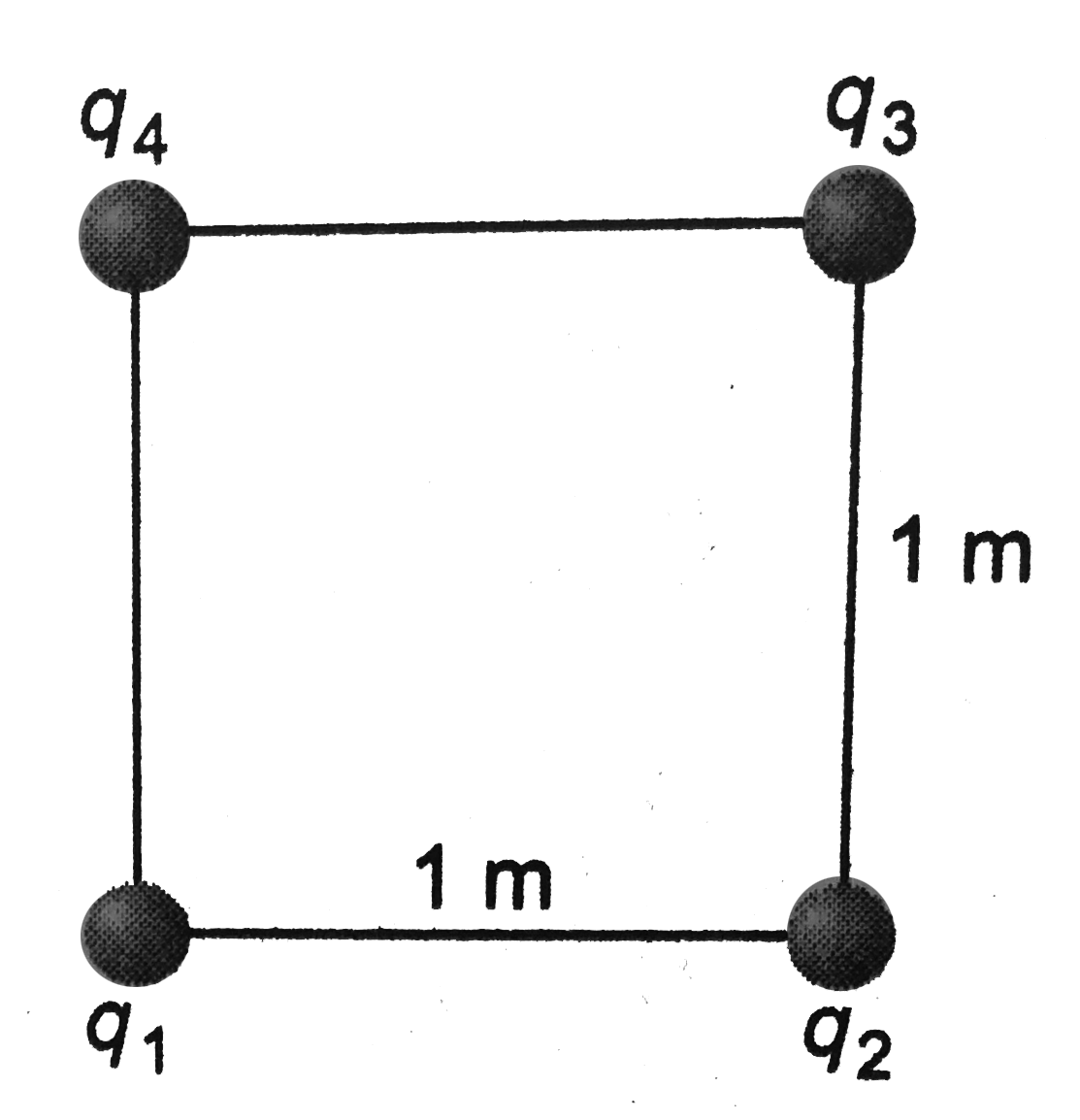
Four charges q1=1μC,q2=2μC,q3=−3μCandq4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
To find the electric potential energy of the system of charges placed at the vertices of a square, we can follow these steps:
Step 1: Identify the charges and their positions
We have four charges:
- q1=1μC=1×10−6C
- q2=2μC=2×10−6C
- q3=−3μC=−3×10−6C
- q4=4μC=4×10−6C
These charges are located at the vertices of a square with a side length of 1m.
Step 2: Calculate the potential energy between each pair of charges
The electric potential energy U between two point charges qi and qj separated by a distance r is given by the formula:
Uij=kqiqjr
where k=9×109N⋅m2/C2 is Coulomb's constant.
Step 3: Determine the distances between the charges
In a square of side 1m:
- The distance between charges on adjacent corners (e.g., q1 and q2) is 1m.
- The distance between charges on opposite corners (e.g., q1 and q3) is √2m.
Step 4: Calculate potential energy for each pair
We will calculate the potential energy for each unique pair of charges:
1. Between q1 and q2:
U12=kq1q21=9×109⋅(1×10−6)(2×10−6)1=18×10−3J
2. Between q1 and q3:
U13=kq1q3√2=9×109⋅(1×10−6)(−3×10−6)√2=−27×10−3J
3. Between q1 and q4:
U14=kq1q41=9×109⋅(1×10−6)(4×10−6)1=36×10−3J
4. Between q2 and q3:
U23=kq2q3√2=9×109⋅(2×10−6)(−3×10−6)√2=−27×10−3J
5. Between q2 and q4:
U24=kq2q41=9×109⋅(2×10−6)(4×10−6)1=72×10−3J
6. Between q3 and q4:
U34=kq3q4√2=9×109⋅(−3×10−6)(4×10−6)√2=−54×10−3J
Step 5: Sum the potential energies
Now we sum all the potential energies calculated:
Utotal=U12+U13+U14+U23+U24+U34
Utotal=(18−27+36−27+72−54)×10−3J
Utotal=18×10−3J
Final Answer
The total electric potential energy of the system of charges is:
Utotal=18mJ
We have four charges:
- q1=1μC=1×10−6C
- q2=2μC=2×10−6C
- q3=−3μC=−3×10−6C
- q4=4μC=4×10−6C
The electric potential energy U between two point charges qi and qj separated by a distance r is given by the formula:
Uij=kqiqjr
where k=9×109N⋅m2/C2 is Coulomb's constant.
In a square of side 1m:
- The distance between charges on adjacent corners (e.g., q1 and q2) is 1m.
- The distance between charges on opposite corners (e.g., q1 and q3) is √2m.
We will calculate the potential energy for each unique pair of charges:
U12=kq1q21=9×109⋅(1×10−6)(2×10−6)1=18×10−3J
U13=kq1q3√2=9×109⋅(1×10−6)(−3×10−6)√2=−27×10−3J
U14=kq1q41=9×109⋅(1×10−6)(4×10−6)1=36×10−3J
U23=kq2q3√2=9×109⋅(2×10−6)(−3×10−6)√2=−27×10−3J
U24=kq2q41=9×109⋅(2×10−6)(4×10−6)1=72×10−3J
U34=kq3q4√2=9×109⋅(−3×10−6)(4×10−6)√2=−54×10−3J
Now we sum all the potential energies calculated:
Utotal=U12+U13+U14+U23+U24+U34
Utotal=(18−27+36−27+72−54)×10−3J
Utotal=18×10−3J
The total electric potential energy of the system of charges is:
Utotal=18mJ
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.115videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.215videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
Similar Questions
For charges q1=1μC,q2=2μC,q3=−3μC and q4=4μC are kept on the vertices of a square of side 1m. Find the electric potential energy of this system of charges.
 View Solution
View SolutionThree charges q1=1μC,q2=−2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q1.
How to proceed Charge q2 will attract charge q1 (along the line joining them) and charge q3 will repel charge q1. Therefore, two forces will act on q1, one due to q2 and another due to q3. Since , the force is a vector quantity both of these force (say F1 and F2) will be added by vector method. Following are two methods of their addition
 View Solution
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1
 View Solution
View SolutionFour point charges 1μC,3μC,−2μCand−2μC are arranged on the four vertices of a square of side 1 cm. The dipole moment of this charge assembly is
 View Solution
View SolutionCharges 5μC,−2μC,3μCand−9μC are placed at the corners A,B,C and D of a square ABCD of side 1m. The net electric potential at the centre of th square is
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .View Solution
.View SolutionFour charges of 6μC,2μC,−12μCand4μC are placed at the corners of a square of side 1m. The square is in x-y plane and its centre is at origin. Electric potential due to these charges is zero everywhere or the line
View SolutionFour identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .View Solution
.View SolutionElectric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
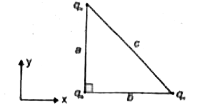
View SolutionSuppose that three point charges qa,qb and qc are arranged at the vertices of a right -angled triangle as shown . What is the absolute electric potential at the position of the third charge if qa=−6.0μC,qb=+4.0μC,qc=+2.0μC,a=4.0m and b=3.0 m ? Suppose that the third charge which is initially at rest is repelled to infinity by the combined electric field of the other two charges which are held fixed . What is the final final kinetic energy of the third charge ?
 View Solution
View Solution

