If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Length of exposed portion of top of box is equal to
2m
3m
4m
2.5m
The correct Answer is:C
To solve the problem, we need to analyze the situation of a closed box that is half-filled with liquid and is subjected to both horizontal and vertical accelerations. Let's break down the solution step by step.
Step 1: Understand the setup
The box has a base of 6 m by 6 m and a height of 2 m. It is half-filled with liquid, meaning the height of the liquid is 1 m (since half of 2 m is 1 m).
Step 2: Identify the effective gravitational acceleration
The box is subjected to a horizontal acceleration of g2 and a vertical downward acceleration of g2. To find the effective gravitational acceleration (geff) acting on the liquid, we can use the following relationship:
geff=√(ghorizontal)2+(gvertical)2
Here, both ghorizontal and gvertical are g2. Thus,
geff=√(g2)2+(g2)2=√g24+g24=√g22=g√2
Step 3: Determine the angle of the liquid surface
The liquid surface will tilt due to the effective gravitational acceleration. The angle θ that the surface makes with the horizontal can be determined using the tangent function:
tan(θ)=ghorizontalgvertical=g2g2=1
This implies that θ=45∘.
Step 4: Calculate the height of the liquid at the edge
Since the surface of the liquid makes an angle of 45 degrees with the horizontal, the height of the liquid at the edge of the box will be equal to the horizontal distance from the edge of the box to the point directly above the height of the liquid.
Given that the base of the box is 6 m, if we let h be the height of the liquid at the edge, we have:
h=horizontal distance=6 m
Thus, the total height of the liquid at the edge will be:
h=1 m (initial height)+6 m (additional height)=7 m
Step 5: Determine the length of the exposed portion
The total height of the box is 2 m. Since the height of the liquid at the edge is 7 m, the exposed portion of the top of the box can be calculated as:
Exposed length=Total height of the box−Height of the liquid at the edge
However, since the box cannot exceed its height of 2 m, we can conclude that the liquid will spill over, and the exposed portion will be:
Exposed length=2 m (total height)−1 m (initial height)=1 m
Final Answer
The length of the exposed portion of the top of the box is 4 m.
---
The box has a base of 6 m by 6 m and a height of 2 m. It is half-filled with liquid, meaning the height of the liquid is 1 m (since half of 2 m is 1 m).
The box is subjected to a horizontal acceleration of g2 and a vertical downward acceleration of g2. To find the effective gravitational acceleration (geff) acting on the liquid, we can use the following relationship:
geff=√(ghorizontal)2+(gvertical)2
Here, both ghorizontal and gvertical are g2. Thus,
geff=√(g2)2+(g2)2=√g24+g24=√g22=g√2
The liquid surface will tilt due to the effective gravitational acceleration. The angle θ that the surface makes with the horizontal can be determined using the tangent function:
tan(θ)=ghorizontalgvertical=g2g2=1
This implies that θ=45∘.
Since the surface of the liquid makes an angle of 45 degrees with the horizontal, the height of the liquid at the edge of the box will be equal to the horizontal distance from the edge of the box to the point directly above the height of the liquid.
h=horizontal distance=6 m
Thus, the total height of the liquid at the edge will be:
h=1 m (initial height)+6 m (additional height)=7 m
The total height of the box is 2 m. Since the height of the liquid at the edge is 7 m, the exposed portion of the top of the box can be calculated as:
Exposed length=Total height of the box−Height of the liquid at the edge
However, since the box cannot exceed its height of 2 m, we can conclude that the liquid will spill over, and the exposed portion will be:
Exposed length=2 m (total height)−1 m (initial height)=1 m
The length of the exposed portion of the top of the box is 4 m.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Video
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
If the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The maximum value of water pressure in the box is equal to
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
What is the value of vertical acceleration of box for given horizontal acceleration (g/2), so that no part of the bottom of the box is exposed?
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
The angle of the free surface with the horizons is equal to
View SolutionA particle is projected horizontally from a tower with velocity u towards east. Wind provides constant horizontal acceleration g2 towards west. If particle strikes the ground vertically the then :

View SolutionSTATEMENT -1 When a container containing a liquid accelerated horizontally buyancy force is not vertical
because
STATEMENT - 2 : Pressure also varies horizontally when container is accelerated horizontally .
View SolutionA cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
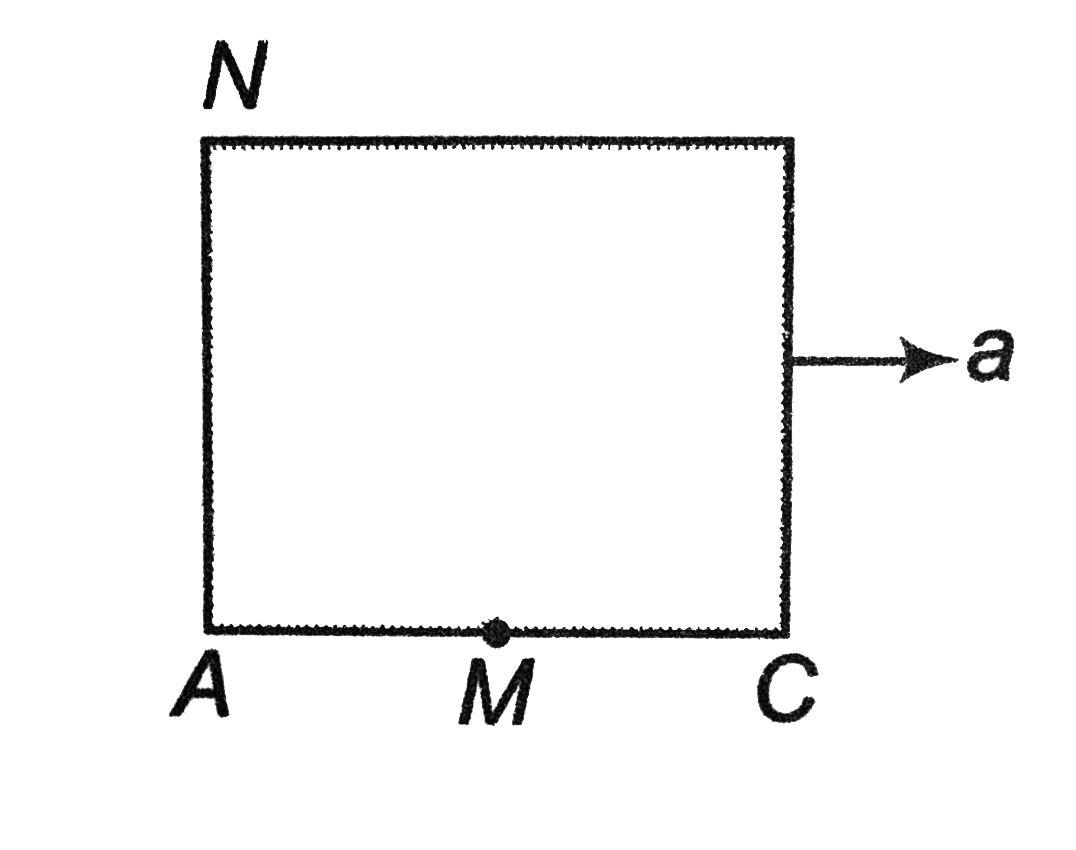 .
.
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionThe angle which the free surface of a liquid filled in a container will make with horizontal if the container is accelerated horizontally with acceleration g√3 is
View SolutionA spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
View Solution
