In a potentiometer arrangement for determining the emf of cell, the balance point of the cell in open circuit is 350 cm. When a resistance of 9Ω is used in the external circuit of cell , the balance point shifts to 300 cm. Determine the internal resistance of the cell.
To determine the internal resistance of the cell using the given potentiometer arrangement, we can follow these steps:
1. Identify the Given Data:
- Length of the wire at balance point in open circuit, L1=350cm
- Length of the wire at balance point with external resistance, L2=300cm
- External resistance, R=9Ω
2. Understand the Potentiometer Principle:
- The potential gradient (K) is defined as the EMF (E) of the cell divided by the length of the wire (L) when the circuit is open:
K=EL1
3. Calculate the Potential Gradient in Both Cases:
- When the circuit is closed with the external resistance:
K=VL2=E−IrL2
- Here, V is the terminal potential difference when the circuit is closed, I is the current flowing through the circuit, and r is the internal resistance of the cell.
4. Express Current in Terms of External Resistance and Internal Resistance:
- The current I can be expressed as:
I=ER+r
5. Set Up the Equation:
- From the two expressions for the potential gradient, we can equate them:
EL1=E−IrL2
6. Substituting Current into the Equation:
- Substitute I in the equation:
EL1=E−(ER+r)rL2
7. Cross-Multiply and Rearrange:
- Cross-multiply to eliminate the fractions:
E⋅L2=L1⋅(E−ErR+r)
- Expand and rearrange to isolate terms involving r.
8. Solve for Internal Resistance r:
- After simplification, you will find:
r=R⋅(L1−L2)L2
- Substitute the known values:
r=9⋅(350−300)300
r=9⋅50300=450300=1.5Ω
Final Answer:
The internal resistance of the cell is r=1.5Ω.
---
- Length of the wire at balance point in open circuit, L1=350cm
- Length of the wire at balance point with external resistance, L2=300cm
- External resistance, R=9Ω
- The potential gradient (K) is defined as the EMF (E) of the cell divided by the length of the wire (L) when the circuit is open:
K=EL1
- When the circuit is closed with the external resistance:
K=VL2=E−IrL2
- Here, V is the terminal potential difference when the circuit is closed, I is the current flowing through the circuit, and r is the internal resistance of the cell.
- The current I can be expressed as:
I=ER+r
- From the two expressions for the potential gradient, we can equate them:
EL1=E−IrL2
- Substitute I in the equation:
EL1=E−(ER+r)rL2
- Cross-multiply to eliminate the fractions:
E⋅L2=L1⋅(E−ErR+r)
- Expand and rearrange to isolate terms involving r.
- After simplification, you will find:
r=R⋅(L1−L2)L2
- Substitute the known values:
r=9⋅(350−300)300
r=9⋅50300=450300=1.5Ω
The internal resistance of the cell is r=1.5Ω.
Topper's Solved these Questions
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C50videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - PHYSICS (Theory) DELHI BOARD -2016 [SET -I][COMPTT.]11videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-A28videos
XII BOARDS
- BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D6videos
SAMPLE PAPER 2019
Similar Questions
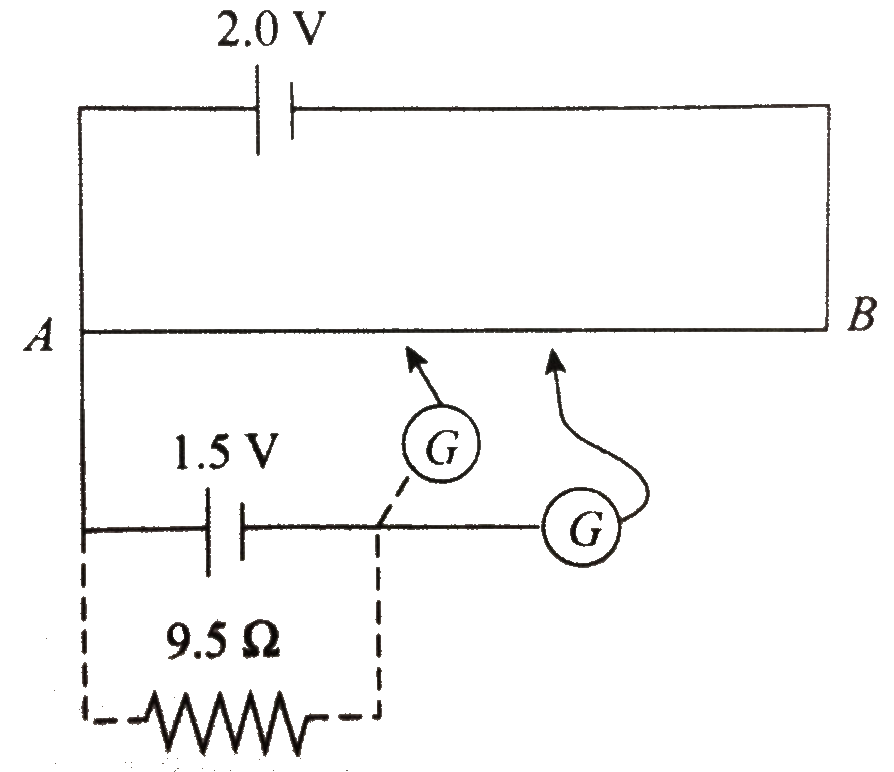
Figure 6.13 shows a 2.0V potentiometer used for the determination of internal resistance of a 1.5V cell. The balance point of the cell in open circuit is 76.3cm. Whan a resistor of 9.5Ω is used in the external circuit of the cell, the balance point shifts to 64.8cm, length of the potentiometer. Dentermine the internal resistance of the cell.
 View Solution
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View Solution
Knowledge Check
- Question 1 - Select One
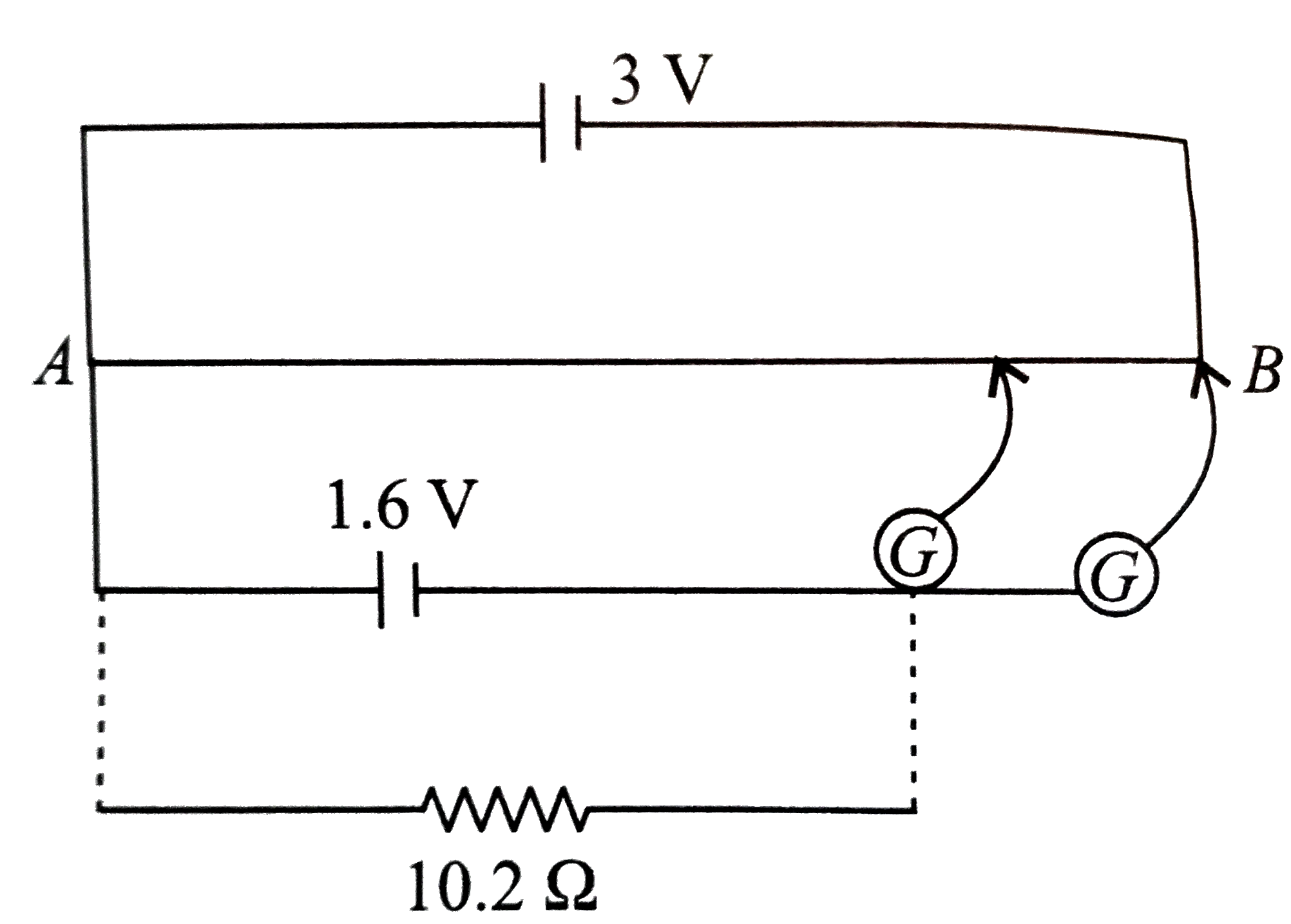
3V poteniometer used for the determination of internal resistance of a 2.4V cell. The balanced point of the cell in open circuit is 75.8cm. When a resistor of 10.2Ω is used in the external circuit of the cell the balance point shifts to 68.3cm length of the potentiometer wire. The internal resistance of the cell is
 A2.5ΩB2.25ΩC1.12ΩD3.2Ω
A2.5ΩB2.25ΩC1.12ΩD3.2Ω
In a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionIn an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
View SolutionIn an experiment with a potentiometer, the null point is
obtained at a distance of 60cm along the wire from the
common terminal with a leclanche cell. When a shunt
resistance of 1Ω is connected across the cell, the null
point shifts to a distance of 30cm from the common
terminal. what is the internal resistance of the cell?View SolutionA battery is connected to a potentiometer and a balance point is obtained at 84cm along the wire. When its terminals are connected by a 5Ω resistor, the balance point changes to 70cm.
Calculate the internal resistance of the cell.View SolutionIn the potentiometer circuit shown in the figure the balance length AJ=60cm when switch S is open. When switch S is closed and the value of R=5Ω, the b alance length AJ=50cm. The internal resistance of the cell C' is
 View Solution
View SolutionFor the given circuit,
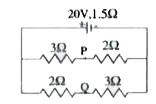
If internal resistance of cell is 1.5Ω, thenView Solution

