In C−R circuit, answer the following two questions
Dielectric constant of the slab between plates of a capacitor is 18 and its resistivity is (4π×103)Ω−m. Then time constant of this capacitor when directly connected to a battery will be
2μs
3μs
1μs
9μs
The correct Answer is:A
To find the time constant of the capacitor in the given C−R circuit, we will follow these steps:
Step 1: Understand the formula for time constant
The time constant (τ) of an RC circuit is given by the formula:
τ=R×C
where R is the resistance and C is the capacitance.
Step 2: Calculate the resistance (R)
The resistance R of the material can be calculated using the formula:
R=ρ⋅lA
where:
- ρ is the resistivity of the material,
- l is the length of the conductor,
- A is the cross-sectional area.
Step 3: Calculate the capacitance (C)
The capacitance C of the capacitor can be calculated using the formula:
C=k⋅A⋅ϵ0d
where:
- k is the dielectric constant,
- A is the area of the plates,
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m),
- d is the distance between the plates.
Step 4: Combine the formulas
Since the area A and length l will cancel out when substituting R and C into the time constant formula, we can simplify:
τ=R×C=(ρ⋅lA)×(k⋅A⋅ϵ0d)
This simplifies to:
τ=ρ⋅k⋅ϵ0⋅ld
Step 5: Substitute the known values
Given:
- ρ=4π×103Ω⋅m
- k=18
- ϵ0=8.85×10−12F/m
We can substitute these values into the equation:
τ=ρ⋅k⋅ϵ0
Since l/d cancels out, we can directly calculate:
τ=(4π×103)⋅18⋅(8.85×10−12)
Step 6: Perform the calculation
Calculating:
1. 4π≈12.566
2. 12.566×103≈12566
3. 12566×18≈226188
4. 226188×8.85×10−12≈2.000×10−6s
Thus, the time constant τ is approximately:
τ≈2μs
Final Answer
The time constant of the capacitor when directly connected to a battery is 2μs.
---
The time constant (τ) of an RC circuit is given by the formula:
τ=R×C
where R is the resistance and C is the capacitance.
The resistance R of the material can be calculated using the formula:
R=ρ⋅lA
where:
- ρ is the resistivity of the material,
- l is the length of the conductor,
- A is the cross-sectional area.
The capacitance C of the capacitor can be calculated using the formula:
C=k⋅A⋅ϵ0d
where:
- k is the dielectric constant,
- A is the area of the plates,
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m),
- d is the distance between the plates.
Since the area A and length l will cancel out when substituting R and C into the time constant formula, we can simplify:
τ=R×C=(ρ⋅lA)×(k⋅A⋅ϵ0d)
This simplifies to:
τ=ρ⋅k⋅ϵ0⋅ld
Given:
- ρ=4π×103Ω⋅m
- k=18
- ϵ0=8.85×10−12F/m
τ=ρ⋅k⋅ϵ0
Since l/d cancels out, we can directly calculate:
τ=(4π×103)⋅18⋅(8.85×10−12)
Calculating:
1. 4π≈12.566
2. 12.566×103≈12566
3. 12566×18≈226188
4. 226188×8.85×10−12≈2.000×10−6s
τ≈2μs
The time constant of the capacitor when directly connected to a battery is 2μs.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Matrix Matching
2 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the plates
View SolutionAssertion : If the distance between parallel plates of a capacitor is halved and dielectric constant is made three times, then the capacitance becomes 6 times.
Reason : Capacity of the capacitor depends upon the nature of the material between the plates.
View Solution
Knowledge Check
A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the platesAC=ε0Ad(K+34K)BC=ε0Ad(2KK+3)CC=ε0Ad(KK+3)DC=ε0Ad(4KK+3)
The space between the plates of a parallel plate capacitor is completely filled with a material of resistivity 2×1011Ωm and dielectric constant 6. Capacity of the capacitor with the given dielectric medium between the plates is 20μF. Find the leakage current if a potential difference 2500V is applied across the capacitor.
View SolutionA parallel plate capacitor has plate of length 'l' width 'w' and separation of plates is 'd' . It is connected to a battery of emf V . A dielectric slab of the same thickness 'd' and of dielectric constant k=4 is being inserted between the plates of the capacitor . At what lenght of the slab inside plates , will the energy stored in the capacitor be two time the initial energy stored ?
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
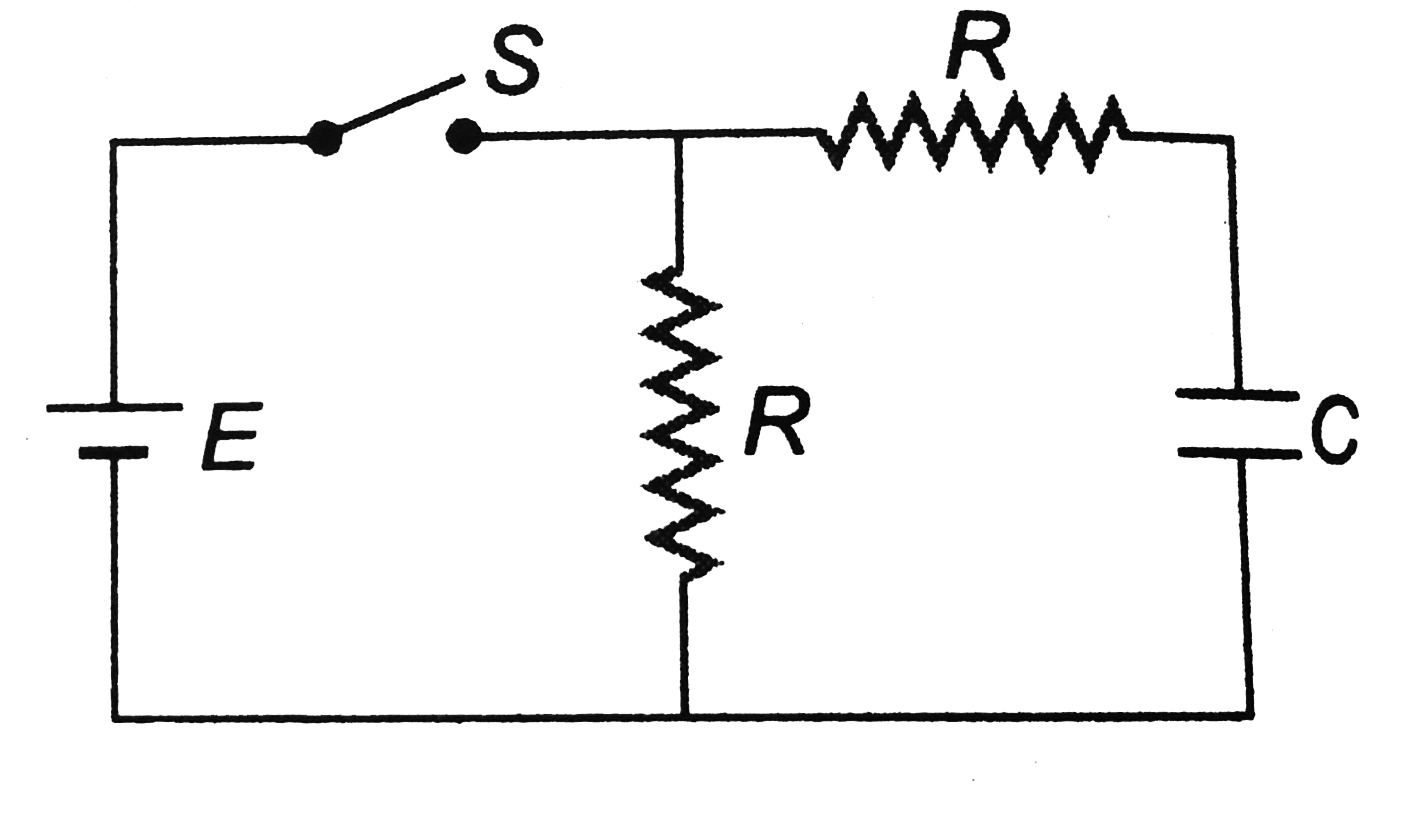
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
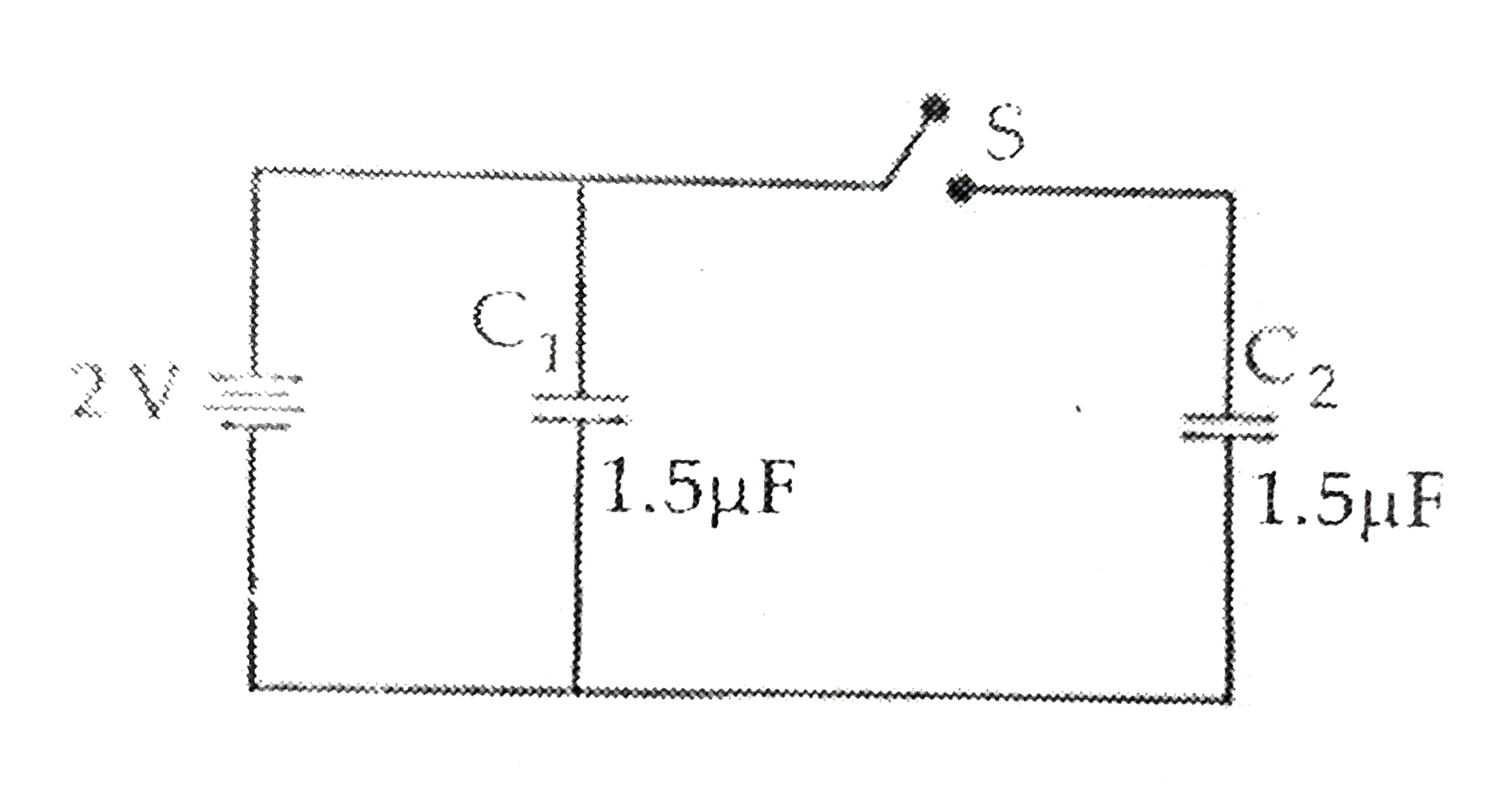
View SolutionFigure shows two identical caoacitors C1andC2 each of 1.5μF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
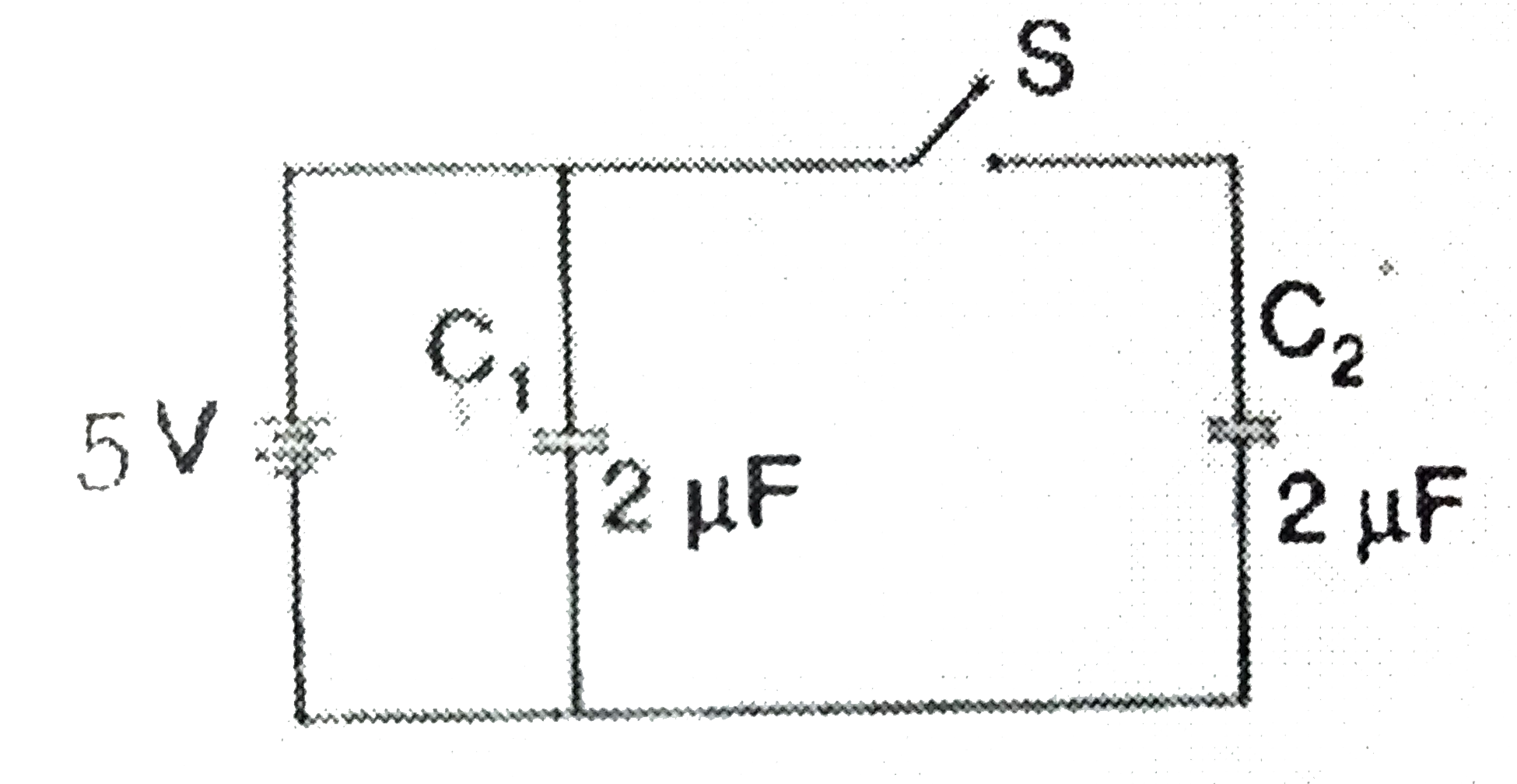
View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
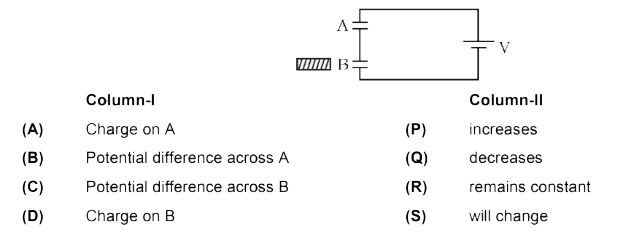
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution
