In Fig. an electron (e) is to be released from rest on the central axis of a uniformly charged disk of radius R. The surface charge density on the disk is +5.00μC/m2. What is the magnitude of the electron's initial acceleration if it is released at a distance (a) R, (b) R/100, and (c ) R/1000 from the center of the disk ? (d) Why does the acceleration magnitude increase only slightly as the release point is moved closer to the disk ?
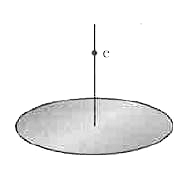
(a) 1.45×1016m/s2, (b) 4.93×1016m/s2, (c ) 4.96×1016m/s2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionAt what distance along the central perpendicular axis of a uniformly charged plastic disk of radius 0.600 m is the magnitude of the electric field equal to 25% of the magnitude of the field at the center of the surface of the disk ?
View Solution
Knowledge Check
The electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell
The volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of R2 from the centre is
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View SolutionNear an infinitely large flat plate with a surface charge density o on each side, the field strength is** E=δ∈nδ, while the field produced by a point charge at a distance r frorn the chargo is Prove that for a uniformly charged disk with a surface charge density a (on each side), the electric field strength on the axis of the disk is the same as for an infinitely large flat plate if the distances arc small in comparison with the disk's radius R, and is the same as for a point charge if the distances are large ** Usually the value of the field strength given in textbooks is half the one given here, since there it is assumed that the charge is on a geometric plane
View SolutionIf the potential at the center of a uniformly charged sphere of radius R is V then electric field at a distance r from the center of sphere will be (r<R) : -
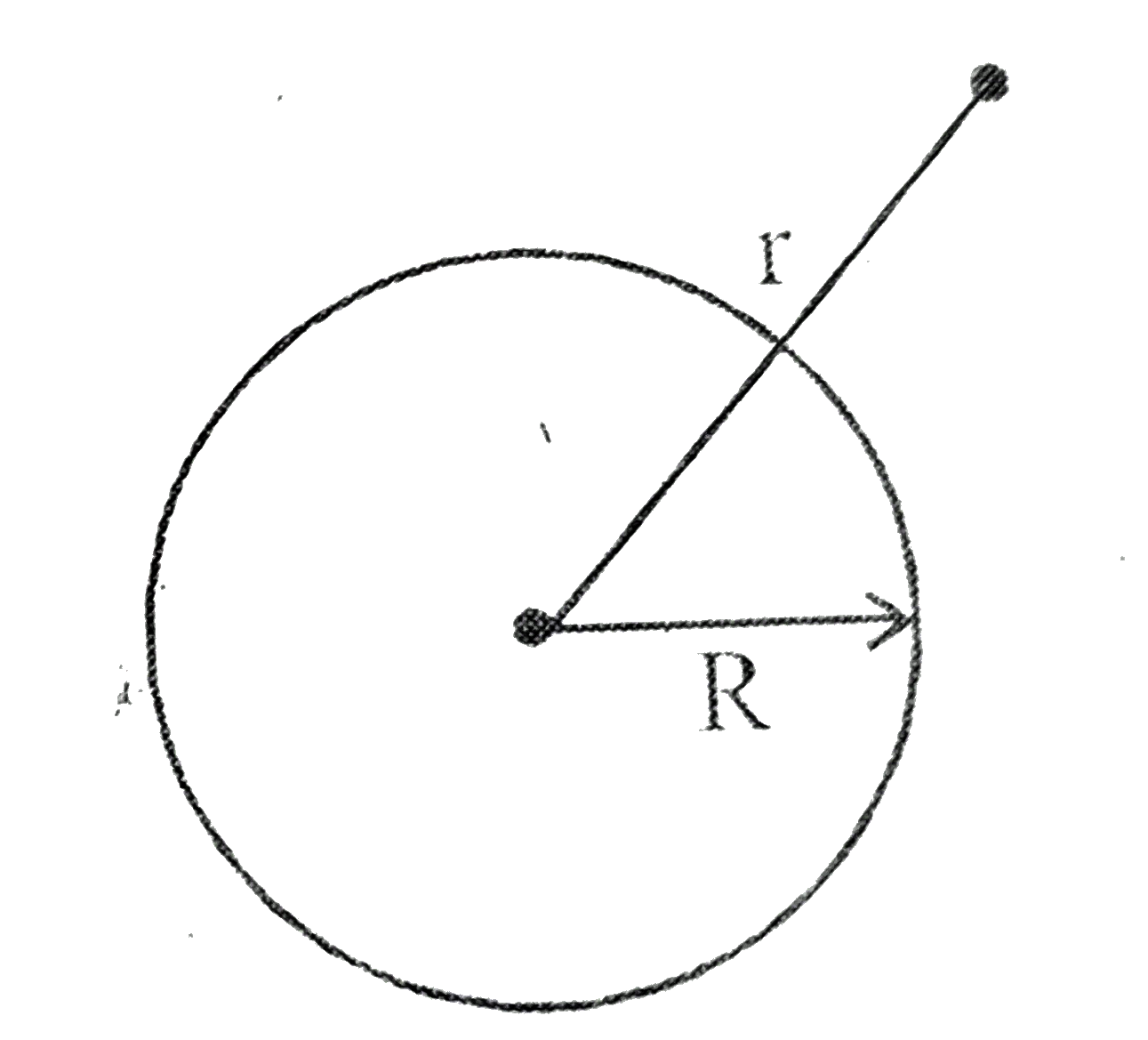
View SolutionCalculate electric field at a point on axis, which at a distance x from centre of uniformly charged disc having surface charge density σ and R which also contains a concentric hole of radius r.
View SolutionA circular hole with radius R/2 is carved from a uniform circular disk of radius R. A smaller disk with radius R/4 with the same uniform density is then put inside the hole as shown in the figure below. The center of mass of the whole system is located at a distance d from the origin. Find d. CM
View Solution
