In the previous question, find maximum velocity and maximum acceleration.
To solve the problem of finding the maximum velocity and maximum acceleration in simple harmonic motion (SHM), we will follow these steps:
Step 1: Identify the given values
From the previous question, we know:
- Amplitude (A) = 1 meter
- Time period (T) = 2 seconds
Step 2: Calculate angular frequency (ω)
The angular frequency (ω) is calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π2=πradians/second
Step 3: Calculate maximum velocity (V_max)
The maximum velocity in SHM is given by the formula:
Vmax=A⋅ω
Substituting the values of A and ω:
Vmax=1⋅π=πmeters/second
Step 4: Calculate maximum acceleration (A_max)
The maximum acceleration in SHM is given by the formula:
Amax=A⋅ω2
Substituting the values of A and ω:
Amax=1⋅(π)2=π2meters/second2
Final Results
- Maximum Velocity (V_max) = π meters/second
- Maximum Acceleration (A_max) = π² meters/second²
From the previous question, we know:
- Amplitude (A) = 1 meter
- Time period (T) = 2 seconds
The angular frequency (ω) is calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π2=πradians/second
The maximum velocity in SHM is given by the formula:
Vmax=A⋅ω
Substituting the values of A and ω:
Vmax=1⋅π=πmeters/second
The maximum acceleration in SHM is given by the formula:
Amax=A⋅ω2
Substituting the values of A and ω:
Amax=1⋅(π)2=π2meters/second2
- Maximum Velocity (V_max) = π meters/second
- Maximum Acceleration (A_max) = π² meters/second²
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Solved Example
15 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
The equation of a transverse wave propagating through a stretched string is given by y=2sin2π(t0.04−x40)
where y and x are in centimeter and t in seconds. Find the velocity of the wave, maximum velocity of the string and the maximum acceleration.
View SolutionA sinusoidal wave propagates along a string. In figure (a) and (b) 'y' represents displacement of particle from the mean postion. 'x' & 't' have usual meanings. Find :-
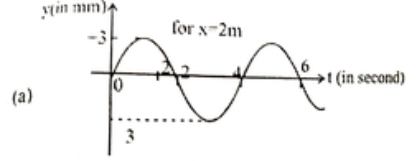
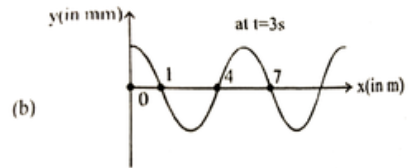
(a) wavelength, frequency and speed of the wave
(b) maximum velocity and maximum acceleration of the particles
View SolutionA particle executes SHM with an amplitude 8cm and a frequency 4Hz initially, in the positive direction , determine its displacement equation and the maximum velocity and acceleration.
View SolutionFor Question , find maximum velocity and maximum acceleration
Hint : Maximum velocity =Aω
Maximum acceleration=Aω2
A particle executes SHM on a straight line path. The amplitude of oscillation is 3cm . magnitude of its acceleration is equal to that of its velocity when its displacement from the mean position is 1cm.
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionIn the previous question, the mean velocity of the rocket reaching the maximum height is :
View SolutionA 0.5kg body performs simple harmonic motion with a frequency of 2Hz and an amplitude of 8mm. Find the maximum velocity of the body, its maximum acceleration and the maximum restoring force to which the body is subjected.
View SolutionA harmonically moving transverse wave on a string has a maximum particle velocity and acceleration of 3 m/s and 90m/s2 respectively. Velocity of the wave is 20m/s. Find the waveform.
View SolutionThe maximum transverse velocity and maximum transverse acceleration of a harmonic wave in a one - dimensional string are 1ms−1and1ms−2 respectively. The phase velocity of the wave is 1ms−1. The waveform is
View Solution
