Let V and E be the gravitational potential field. Then select the correct alternative(s) :
The plot of E against r ( distance form centre) is discontinuous for a spherical shell
The plot of V against r is continuous for a spherical shell
The plot of E against r is discontinuous for a solid sphere
The plot of V against r is continuous for a solid sphere
The correct Answer is:A, B, D
To solve the question regarding the gravitational potential field (V) and gravitational field (E) for a spherical shell and a solid sphere, we will analyze the behavior of these fields with respect to distance (r).
1. Understanding Gravitational Field (E):
- The gravitational field (E) is defined as the force experienced by a unit mass at a point in space due to the gravitational attraction of a mass.
- For a spherical shell, the gravitational field outside the shell behaves like a point mass, while inside the shell, the gravitational field is zero.
2. Graph of E for a Spherical Shell:
- Outside the shell (r > R), the gravitational field E is given by the formula:
E=GMr2
- Inside the shell (r < R), the gravitational field E is:
E=0
- Therefore, the graph of E vs. r for a spherical shell is discontinuous at r = R, where it jumps from 0 to a positive value.
3. Understanding Gravitational Potential (V):
- The gravitational potential (V) is the work done per unit mass in bringing a mass from infinity to a point in space.
- For a spherical shell, the potential inside the shell is constant and equal to the potential at the surface.
4. Graph of V for a Spherical Shell:
- Outside the shell (r > R), the potential is:
V=−GMr
- Inside the shell (r < R), the potential is constant:
V=−GMR
- Thus, the graph of V vs. r for a spherical shell is continuous, with a constant value inside the shell and a decreasing value outside.
5. Graph of E for a Solid Sphere:
- For a solid sphere, the gravitational field inside the sphere (r < R) is given by:
E=GMR3r
- Outside the sphere (r > R), it behaves as:
E=GMr2
- The graph of E vs. r for a solid sphere is continuous, starting from 0 at the center and increasing to a maximum value at the surface.
6. Graph of V for a Solid Sphere:
- For a solid sphere, the potential inside (r < R) is:
V=−GM2R+GMR3r2
- Outside the sphere (r > R), it is:
V=−GMr
- The graph of V vs. r for a solid sphere is also continuous.
Conclusion:
Based on the analysis:
- The plot of E against r for a spherical shell is discontinuous.
- The plot of V against r for both the spherical shell and solid sphere is continuous.
- The plot of E against r for a solid sphere is continuous.
- The plot of V against r for a solid sphere is continuous.
Correct Alternatives:
- A: E against r is discontinuous (True)
- B: V against r is continuous (True)
- C: E against r for solid sphere is discontinuous (False)
- D: V against r for solid sphere is continuous (True)
Thus, the correct options are A, B, and D.
- The gravitational field (E) is defined as the force experienced by a unit mass at a point in space due to the gravitational attraction of a mass.
- For a spherical shell, the gravitational field outside the shell behaves like a point mass, while inside the shell, the gravitational field is zero.
- Outside the shell (r > R), the gravitational field E is given by the formula:
E=GMr2
- Inside the shell (r < R), the gravitational field E is:
E=0
- Therefore, the graph of E vs. r for a spherical shell is discontinuous at r = R, where it jumps from 0 to a positive value.
- The gravitational potential (V) is the work done per unit mass in bringing a mass from infinity to a point in space.
- For a spherical shell, the potential inside the shell is constant and equal to the potential at the surface.
- Outside the shell (r > R), the potential is:
V=−GMr
- Inside the shell (r < R), the potential is constant:
V=−GMR
- Thus, the graph of V vs. r for a spherical shell is continuous, with a constant value inside the shell and a decreasing value outside.
- For a solid sphere, the gravitational field inside the sphere (r < R) is given by:
E=GMR3r
- Outside the sphere (r > R), it behaves as:
E=GMr2
- The graph of E vs. r for a solid sphere is continuous, starting from 0 at the center and increasing to a maximum value at the surface.
- For a solid sphere, the potential inside (r < R) is:
V=−GM2R+GMR3r2
- Outside the sphere (r > R), it is:
V=−GMr
- The graph of V vs. r for a solid sphere is also continuous.
Based on the analysis:
- The plot of E against r for a spherical shell is discontinuous.
- The plot of V against r for both the spherical shell and solid sphere is continuous.
- The plot of E against r for a solid sphere is continuous.
- The plot of V against r for a solid sphere is continuous.
- A: E against r is discontinuous (True)
- B: V against r is continuous (True)
- C: E against r for solid sphere is discontinuous (False)
- D: V against r for solid sphere is continuous (True)
Topper's Solved these Questions
Similar Questions
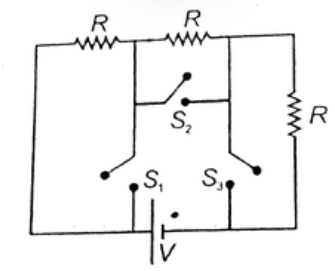
If all the resistors are identical , select the correct alternative (s).
View SolutionLet V and E represent the gravitational potential and field at a distance r from the centre of a uniform solid sphere. Consider the two statements.
A. the plot of V agasinst r is discotinuous
B. The plot of E against r is discontinuous.
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. It is possile to have
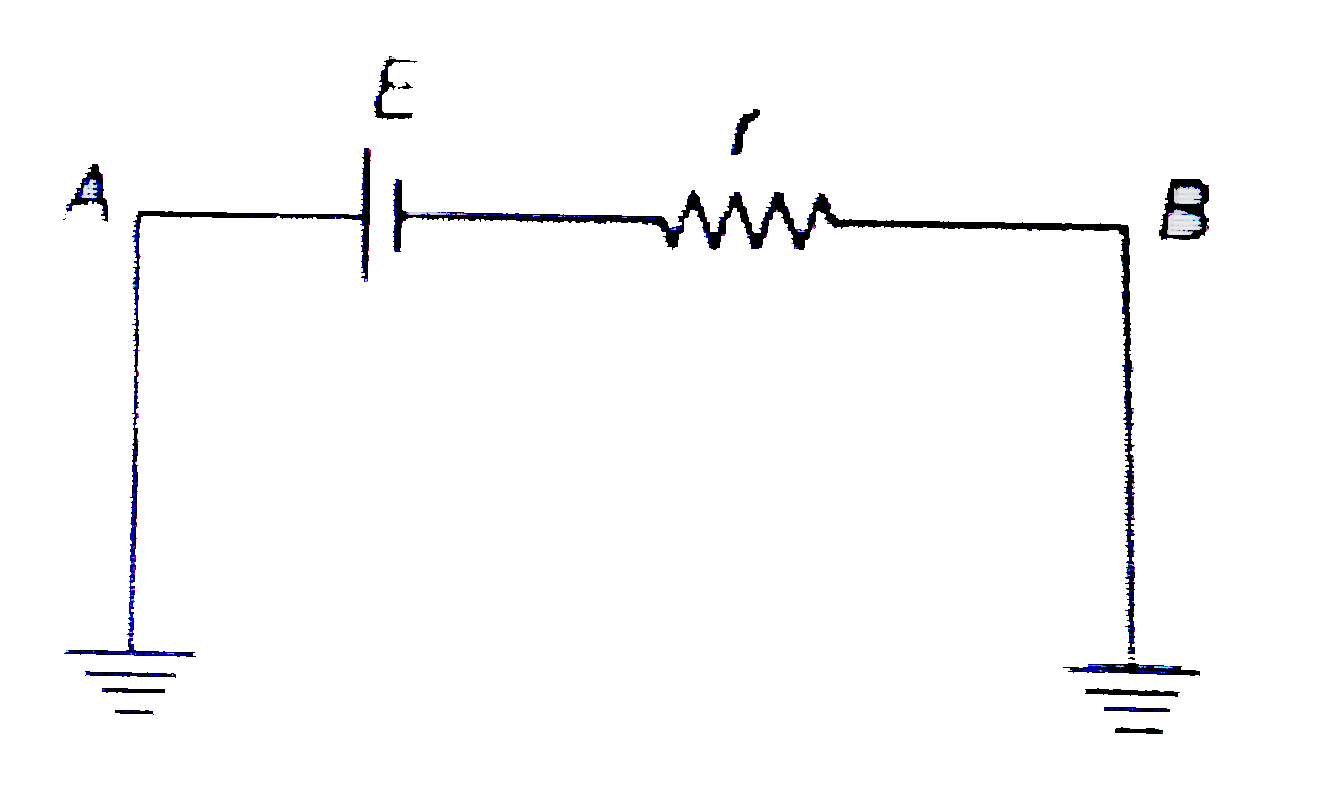
View SolutionBoth terminals of a battery of emf E and internal resistance r are grounded as shown. Select the correct alternative(s).
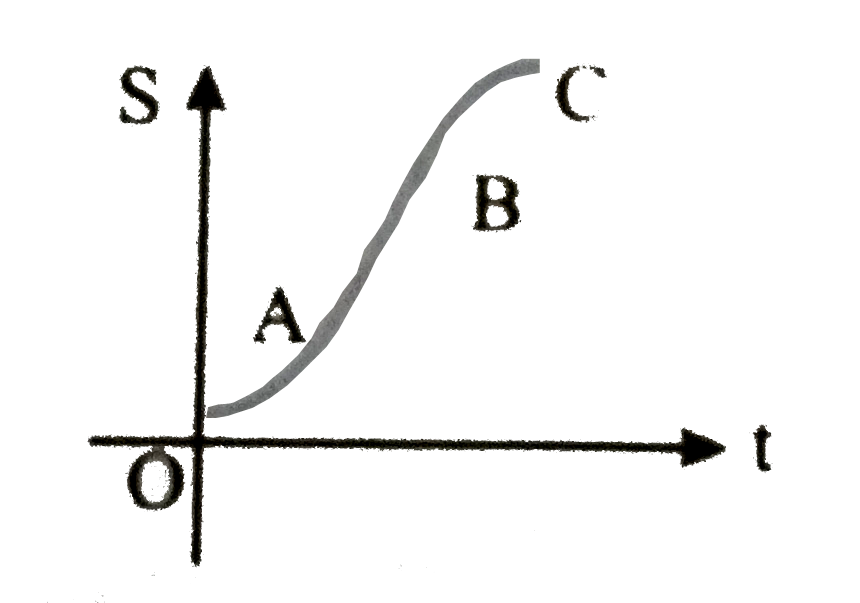
View SolutionDisplacement time graph of a particle moving in a straight line is as shown in figure. Select the correct alternative (s) :
 .
.
View SolutionA particle moves in a straight line with constant acceleration under a constant force F. Select the correct alternative(s).
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
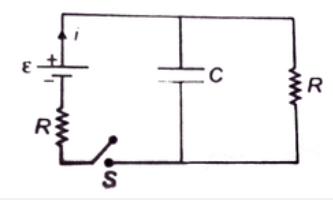
View SolutionIn the circuit shown, the switch is closed at t=0. Select the correct alternative(s)
View SolutionA ball is dropped from height 'h' as shown.The collision is perfectly inelastic. Select the correct alternative (s)
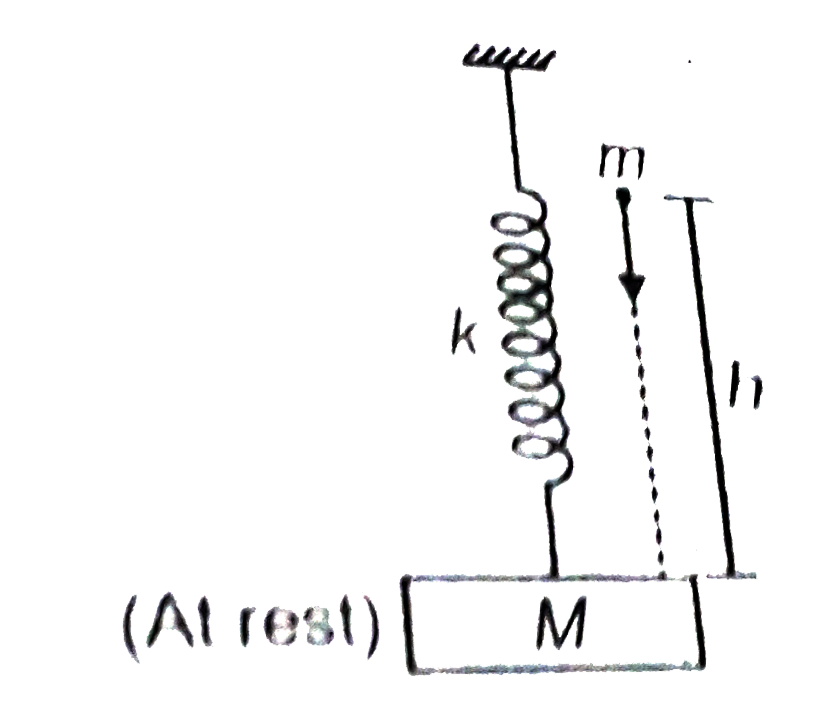
View SolutionA current enters from A and leaves at B through the network shown. Select the correct alternative(s).
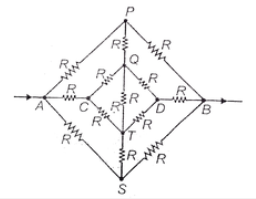
View Solution
