Particles of masses 2M, m and M are respectively at points A, B and C with √GMR(√2+1) is much-much smaller than M and at time t=0, they are all at rest as given in figure
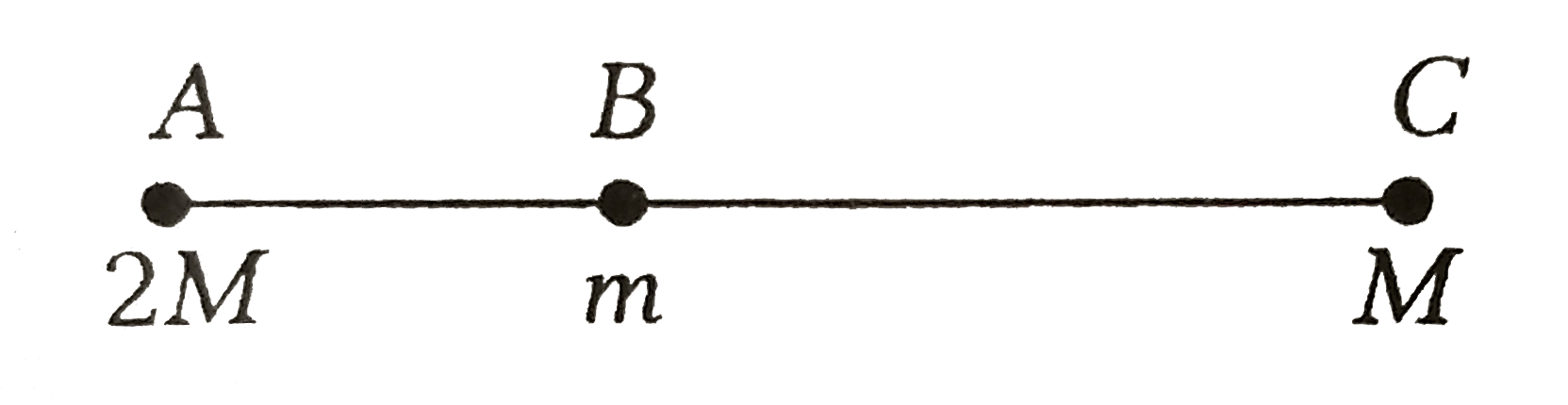
At subsequent time before any collision takes place.
m will remain at rest
m will move towards M
m will move towards 2M
m will have oscillatory motion
The correct Answer is:C
Fore on B due to A =FBA=G(2Mm)(AB)2 towards BA
Force on B due to C =FBC=GMm(BC)2 towards BC
As, (BC)=2AB
⇒FBC=GMm(2AB)2=GMm4(AB)2<FBA
Hence, m will move towards BA (i.e., 2M)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
particles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .
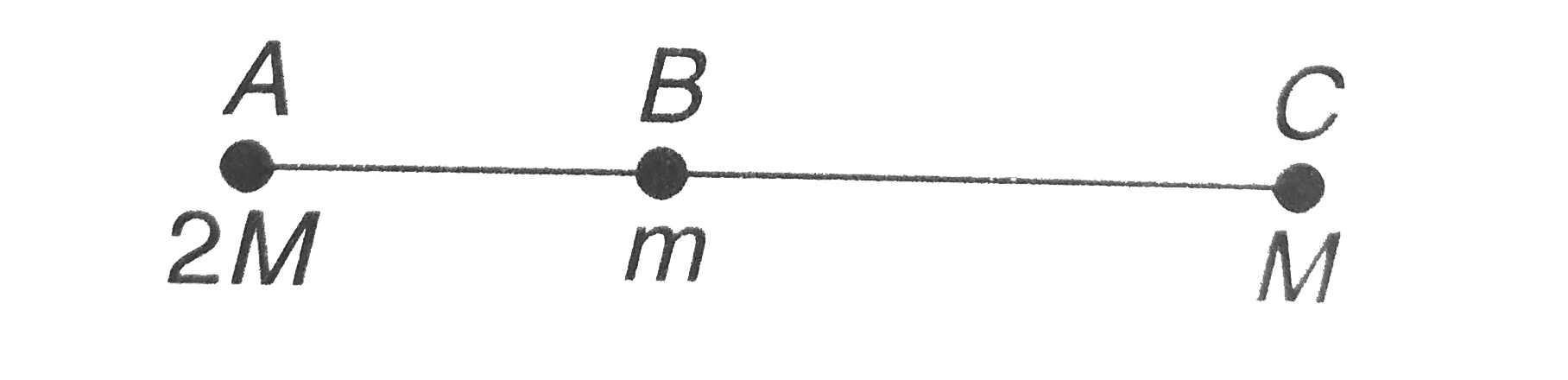
View Solutionparticles of masses 2M m and M are resectively at points A , B and C with AB=12(BC) m is much - much smaller than M and at time t=0 they are all at rest as given in figure . As subsequent times before any collision takes palce .

View SolutionTwo particle of masses m and 2m are coliding elastically as given in figure. If V1 and V2 speed of particle just after collision then
_2019_CBT5_E01_051_Q01.png)
View SolutionFour particles of masses m, 2m, 3m & 4m respectively are placed on the periphery of a circle of radius R as shown in the figure then CM of the system contains the particle is at
View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View Solutionconsider a head on collision between two particles of masses m1andm2. The initial speeds of the particles are u1andu2 in the same direction. The collision starts at t=0 and the particles interact for a time interval △t. during the collision the speed of the first particle varies as
v(t)=u1+t/ t(v1−u1) Find the speed of the second particle as as function of time during the collision.
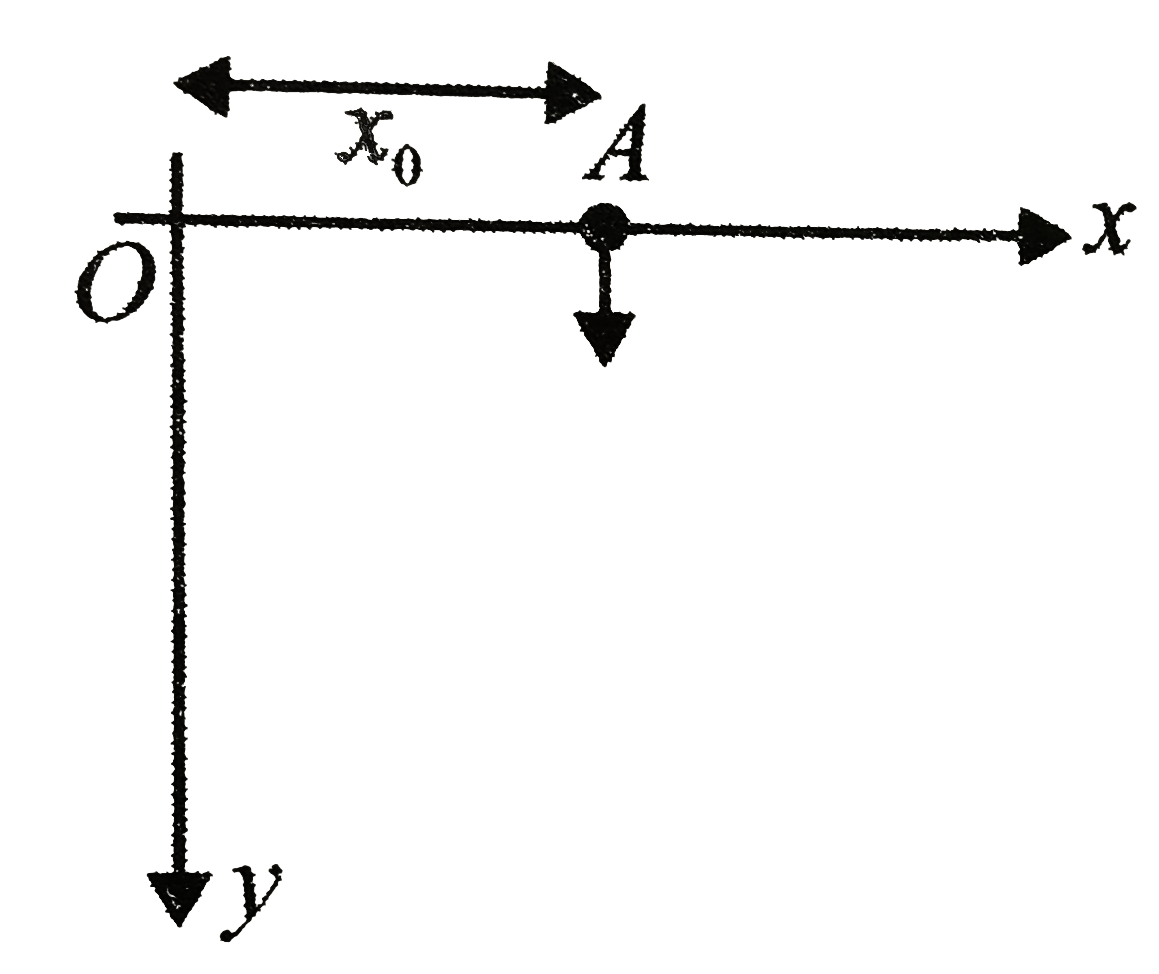
View SolutionA particle of mass m is released from rest at point A in Fig., falling parallel to the (vertical) y-axis. Find the angular momentum of the particle at any time t with respect to the same origin O.
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View SolutionA particle of mass m moving with a speed v hits elastically another staionary particle of mass 2m on a smooth horizontal circular tube of radius r. Find the time when the next collision will take place?
View Solution
