Raindrops of raidus 1mm and mass 4 mg are falling with a speed of 30 m/s on the head of a bald person. The drops splash on the head and come to rest. Assuming equivaletly that the drops cover a distance equal to their radii on the head, estimate the force exerted by the each drop on the head.
To solve the problem step by step, we will follow the principles of physics, specifically using the equations of motion and Newton's second law.
Step 1: Identify the given data
- Radius of the raindrop, r=1mm=1×10−3m
- Mass of the raindrop, m=4mg=4×10−6kg
- Initial velocity of the raindrop, u=30m/s
- Final velocity of the raindrop after splashing, v=0m/s
- Distance covered by the raindrop while coming to rest, s=r=1×10−3m
Step 2: Use the third equation of motion
We can use the third equation of motion to find the acceleration of the raindrop as it comes to rest:
v2=u2+2as
Substituting the known values:
0=(30)2+2a(1×10−3)
This simplifies to:
0=900+2a(1×10−3)
Rearranging gives:
2a(1×10−3)=−900
a=−9002×10−3=−9000.002=−450000m/s2
Step 3: Calculate the force exerted by the raindrop
Using Newton's second law, F=ma:
F=m⋅a
Substituting the values:
F=(4×10−6kg)⋅(−450000m/s2)
Calculating this gives:
F=−1.8N
The negative sign indicates that the force is acting in the opposite direction of the raindrop's motion, which is expected as it comes to rest.
Step 4: Conclusion
The magnitude of the force exerted by each raindrop on the head is:
F=1.8N
- Radius of the raindrop, r=1mm=1×10−3m
- Mass of the raindrop, m=4mg=4×10−6kg
- Initial velocity of the raindrop, u=30m/s
- Final velocity of the raindrop after splashing, v=0m/s
- Distance covered by the raindrop while coming to rest, s=r=1×10−3m
We can use the third equation of motion to find the acceleration of the raindrop as it comes to rest:
v2=u2+2as
Substituting the known values:
0=(30)2+2a(1×10−3)
This simplifies to:
0=900+2a(1×10−3)
Rearranging gives:
2a(1×10−3)=−900
a=−9002×10−3=−9000.002=−450000m/s2
Using Newton's second law, F=ma:
F=m⋅a
Substituting the values:
F=(4×10−6kg)⋅(−450000m/s2)
Calculating this gives:
F=−1.8N
The negative sign indicates that the force is acting in the opposite direction of the raindrop's motion, which is expected as it comes to rest.
The magnitude of the force exerted by each raindrop on the head is:
F=1.8N
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective 2
9 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMACHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Short Answer
15 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
Similar Questions
A water droplet 4.0 mm in diameter is falling with a speed of 10 km/h at an altitude of 20 km. Another droplet 6.0 mm in diameter is falling at 25% of that speed and at 25% of that altitude. The density of air at 20 km is 0.20kg/m3and that at 5.0 km is 0.70kg/m3 Assume that the drag coefficient C is the same for the two drops. Find the ratio of the drag force on the higher drop to that on the lower drop.
View SolutionAn iron nail of mass 0.2 kg is dropped from a height h=1m from level of a sand bed. If it penetrates through a distance x=0.1m in the sand before coming to rest. Calculate the average force exerted by the sand on the nail. (Take g=10m/s2)
View Solution
Knowledge Check
The following problems illustrate the effect of a time-dependent force of a large average magnitude which acts on a moving object only for a short duration. Such forces are called 'impulsive' forces. According to the impulse-momentum theorem, impulse delivered to a body is equal to the change of linear momentum of the body.
A ball of mass 250g is thrown with a speed of 30m/s. The ball strikes a bat and it is hit straight back along the same line at a speed of 50m/s. Variation of the interaction force, as long as the ball remains in contact with the bat, is as shown in Fig.
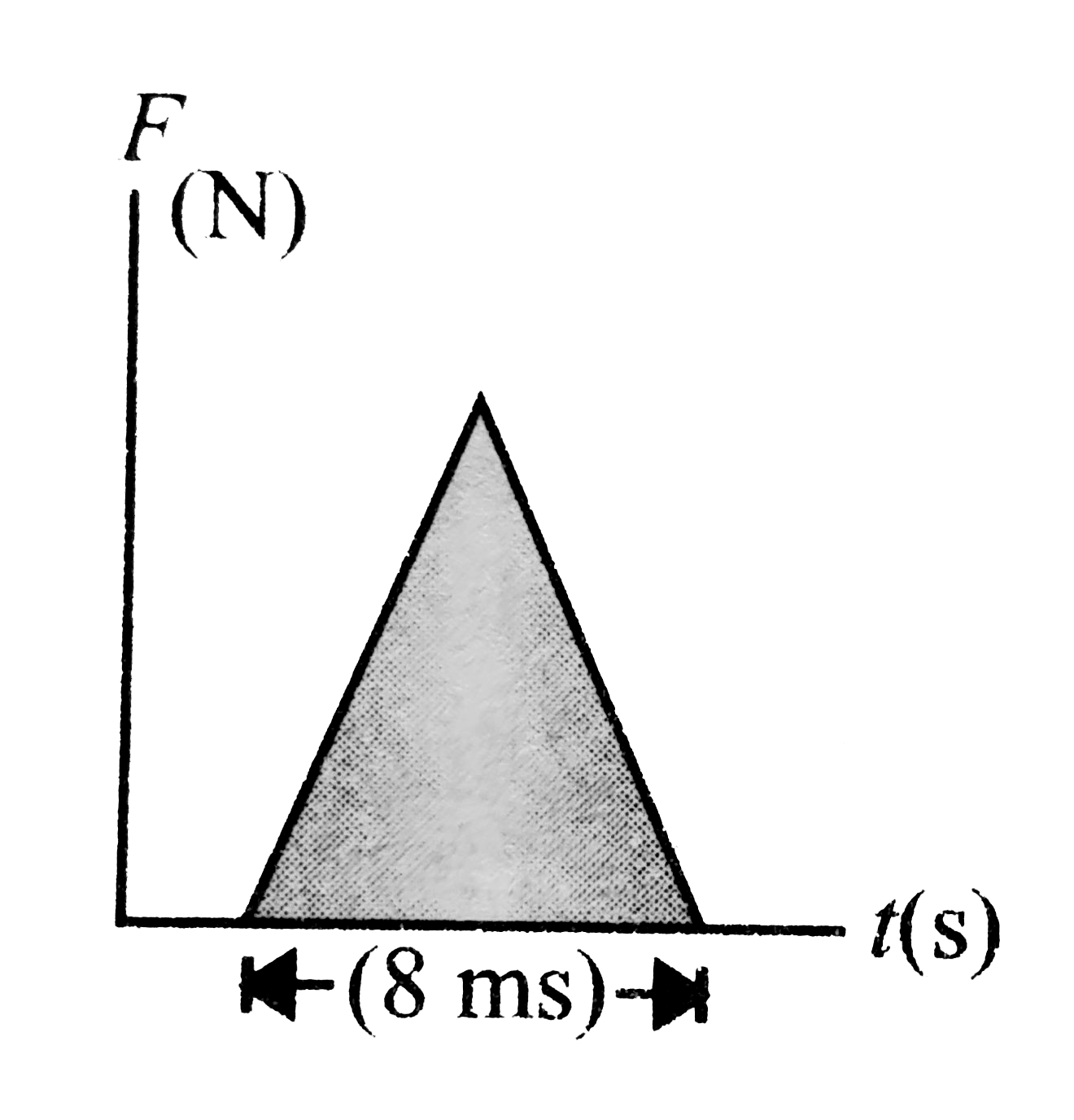
Average force exerted by the bat on the ball is
Let us consider another example. The given ball of mass 250g is dropped from a height 5m on a hard floor. Force exerted by the floor on the ball, as long as these are in contact, varies with time as shown in Fig.
 A5000NB1250NC2500ND7500N
A5000NB1250NC2500ND7500NTwo trains one moving at a speed of 30 mile/h and iother at 60 mile/h, approaching each other. When a faster train blows a whistle, the apparent friequency of the note head by an observer at rest behind the faster train is 1852 Hz. Calculate the frequency of note produced by faster train (Assume speed of sound to be 1100 ft/s)
A2000 vib/sB1500 vib/sC1000 vib/sD2500 vib/sTwo skaters A and B are moving in opposite directions such as they collide head - on and immediately become entangled. Skater A has a mass of 40 kg and is moving with a velocity 4 m/s eastwards while the other skater B has a mass of 60 kg and is moving with a velocity 3 m/ westwards. Assume that hte frictional force acting between the skaters and the ground is negligible

The velocity with which the two entangled skaters will move after collision isA0.2ms−1B0.1ms−1C2ms−1D1ms−1
Figure shows an assembly of deflecting plates A and B ofan ink-jet printer which causes moving ink droplets to deflect at desired displacements by continuously varying electric field between the plates. An ink drop with a mass m=1.3×10−10kg and a negative charge of magnitude q=1.5xx10−13C enters the region between the plates, initially moving along the x-axis with speed vx,=18m/s. The length of plates is L=1.6cm. The plates are connected with a varying voltage and thus produce an electric field at all points between them. Assume that field →E for some duration is constant and it is acting in downward direction as shown and has a magnitude of E=I.4×106N/C, find the vertical deflection of the drop at the far edge ofthe plate? As the gravitational force on the drop is very small relative to the electrostatic force acting on the drop, it can be neglected for this analysis. [6.4×10−4m]

View SolutionA raindrop of radius 0.2 mm falls through air: If the viscosity of air is 18 ×10−6 Pl, find the viscous drag acting on the drop when its speed is 1 m s−1.
View SolutionA raindrop of mass 1 g falling from a height of 1 km hits the ground with a speed of 50ms−1. If the resistive force is proportional to the speed of the drop, then the work done by the resistive force is (Take g=10ms−2)
View SolutionConsider a drop of rain water having mass 1 g falling from a height of 1km. It hits the ground with a speed of 50m/s Take g constant with a volume 10m/s2. The work done by the
(i) gravitational force and the
(ii) resistive force of air is :
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View Solution
