State Gauss' theorem in electrostatics. Derive an expression for the electric field intensity at any point of to an infinite plane sheet of charge.Solution in Punjabi
Gauss.s Theorem : It states that total electric flux through a closed surface enclosing a charge is equal to 1ε0 times the magnitude of charge enclosed. Mathematical form of Gauss.s Las :
Electric flux =ϕ=∮→E.−→dSqε0
Electric field intensity due to an infinite plane thin sheet of charge :
Consider a thin, infinite plane sheet of charge.
Let σ = Surface charge density on both sides
Consider a point P at a distance r from the sheet.
Draw a cylindrical Gaussian surface of cross - section S through the point P with lenght r on each side of the cap.
Electric field E is perpendicular to its end circular Cpas I and II.
Charge enclosed by the Gaussian surface = q=σS
Using Gauss.s theorem
∮→E.−→dS=qε0=σSε0
Gaussian surface is divided into three parts, I II and III
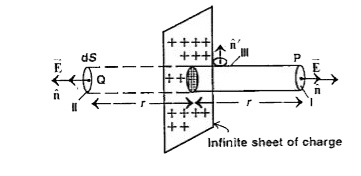
∴ Eqn. (i) becomes ∮I→E.−→dS+II–––∮→E.−→dS+∮III→E.−→dS=σSε0
Angle between →Eand−→dS is 90∘ for the curved III. In this case ∮III→E.−→dS=E.dScos90∘=0
Hence eqn. (ii) becomes ∮I→E.−→dS=undereset(II)∮→E.−→dS=σSε0
Since angle between →Eand−→dS for surface I and II is zero, so
∮I→E.dScos0∘+∮IIE.dScos0∘=σSε0or∮IE.dS+∮IIEdS=σSε0
Since electric field intensity E is Constant at very point of the Gaussian surface so
∴E∮IdS+E∮IIdS=σAε0orES+ES=σSε0[∴∮dS=S=Area of end cap]
or 2ES=σε0
or E=σ2ε0
If the plane sheet has a finite thickness : then charges on both sides of the sheet are to be considered. Thus equation (i) is written as ∫→E.−→dS=2σSε0
Then above eqn. becomes 2ES = 2simgmaε0 i.e., E=σε0 [theregore∫→E.−→dS=2ES]
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - GAUSS'S THEOREMEXERCISE - MOST EXPECTED NUMERICALS4videos
GAUSS'S THEOREM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - GAUSS'S THEOREMEXERCISE - SHORT ANSWER TYPE QUESTIONS8videos
GAUSS'S THEOREM
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CURRENTEXERCISE - NUMERICAL PROBLEMS10videos
FORCE ON A CURRENT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - HUYGENS' PRINCIPLEEXERCISE - LONG ANSWER TYPE QUESTIONS11videos
HUYGENS' PRINCIPLE
Similar Questions
A box encloses an electric dipole of 3μCand−3C, if the dipole length is 6 cm, then find total electric flux associated with box.
12:34View SolutionWhat is the use of Gaussian surface in electrostatics ?
12:13View SolutionA currentof 5.0 A is flowing in eah of the two parallel conductors of infinite length separated by certain distance apart in vacuum in the same directions. Each conductor expereinces a force of 2×10−4Nm−1 due to the other. Find the separation between the two conductors.
07:56View SolutionState Huygen's principle of propagation of light and prove the laws (Snell's law) of refraction on its basis.
04:23View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
04:53View Solutionस्थिर विद्युत् के अन्तर्गत गॉस का प्रमेय लिखिए एवं सिद्ध कीजिए | आवेश के अनन्त समतल चादर के समीप विद्युत् क्षेत्र की तीव्रता के लिए व्यंजक ज्ञात कीजिए |
09:18View SolutionState Gauss's law in electrostatics. Applying Gauss's law derive the expression for electric intensity due to an infinite plane sheet of charge.
05:17View SolutionState Gauss's theorem in electrostatics. Apply this theorem to derive an expression for electric field intensity at a point outside a uniformly charged thin spherical shell.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
06:31View SolutionState Gauss.,s theorem. Derive an expression for eletric field intensity at a point to an infinite plane sheet of charges.
14:45View SolutionState Gauss.s theorem in electrostatics. Using it, derive an experssion for electric field intensity at a point due to infinite sheet of charge. How does the electric field change for a thick sheet of charge?
07:45View SolutionState Gauss theorem in electrostatics. Derive the expression for electric field at a point due to an infinitely long straight charged conductor.
06:13View SolutionDerive an expression for an electric field due to a charged infinite plane sheet.
05:02View Solutionस्थिरवैद्युतिकी में गाउस की प्रमेय बताइये । एक अनन्त लम्बे सीधे आवेशित तार के निकट के एक बिन्दु पर विद्युत क्षेत्र तीव्रता के लिये व्यंजक व्युत्पन्न करने के लिये इस प्रमेय का प्रयोग कीजिये।
05:02View SolutionState and prove Gauss. theorem in electrostatics. Apply it to find the electric field intensity due to a charged plane lamina in its neighbourhood.
View SolutionState Gauss' theorem in electrostatics. Apply it to find the electric field intensity due to a charged plane lamina in its neighbourhood.
View Solution

