The acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
v0t+16bt3
v0t+13bt3
v0t+13bt2
v0t+12bt2
The correct Answer is:A
To solve the problem, we need to find the distance traveled by a particle whose acceleration increases linearly with time. We will follow these steps:
Step 1: Understand the relationship between acceleration, velocity, and displacement.
The acceleration a(t) is given as a(t)=bt, where b is a constant. We know that acceleration is the rate of change of velocity with respect to time.
Step 2: Relate acceleration to velocity.
Using the definition of acceleration:
a=dvdt=bt
We can rearrange this to express dv:
dv=btdt
Step 3: Integrate to find velocity.
Now we will integrate both sides. The initial velocity is v0 at t=0, and we want to find the velocity v at time t:
∫vv0dv=∫t0btdt
The left side integrates to:
v−v0
The right side integrates to:
b2t2
Thus, we have:
v−v0=b2t2
Rearranging gives us the final velocity:
v=v0+b2t2
Step 4: Relate velocity to displacement.
We know that velocity v is the rate of change of displacement s:
v=dsdt
Substituting the expression for v:
dsdt=v0+b2t2
Step 5: Integrate to find displacement.
Now we will integrate to find the displacement s:
∫s0ds=∫t0(v0+b2t2)dt
The left side integrates to s, and the right side can be integrated as follows:
s=v0t+b2∫t0t2dt
The integral of t2 is:
t33
Thus, we have:
s=v0t+b2⋅t33
This simplifies to:
s=v0t+bt36
Final Result:
The distance traveled by the particle in time t is:
s=v0t+bt36
The acceleration a(t) is given as a(t)=bt, where b is a constant. We know that acceleration is the rate of change of velocity with respect to time.
Using the definition of acceleration:
a=dvdt=bt
We can rearrange this to express dv:
dv=btdt
Now we will integrate both sides. The initial velocity is v0 at t=0, and we want to find the velocity v at time t:
∫vv0dv=∫t0btdt
The left side integrates to:
v−v0
The right side integrates to:
b2t2
Thus, we have:
v−v0=b2t2
Rearranging gives us the final velocity:
v=v0+b2t2
We know that velocity v is the rate of change of displacement s:
v=dsdt
Substituting the expression for v:
dsdt=v0+b2t2
Now we will integrate to find the displacement s:
∫s0ds=∫t0(v0+b2t2)dt
The left side integrates to s, and the right side can be integrated as follows:
s=v0t+b2∫t0t2dt
The integral of t2 is:
t33
Thus, we have:
s=v0t+b2⋅t33
This simplifies to:
s=v0t+bt36
The distance traveled by the particle in time t is:
s=v0t+bt36
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.620videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.715videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.415videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
The acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
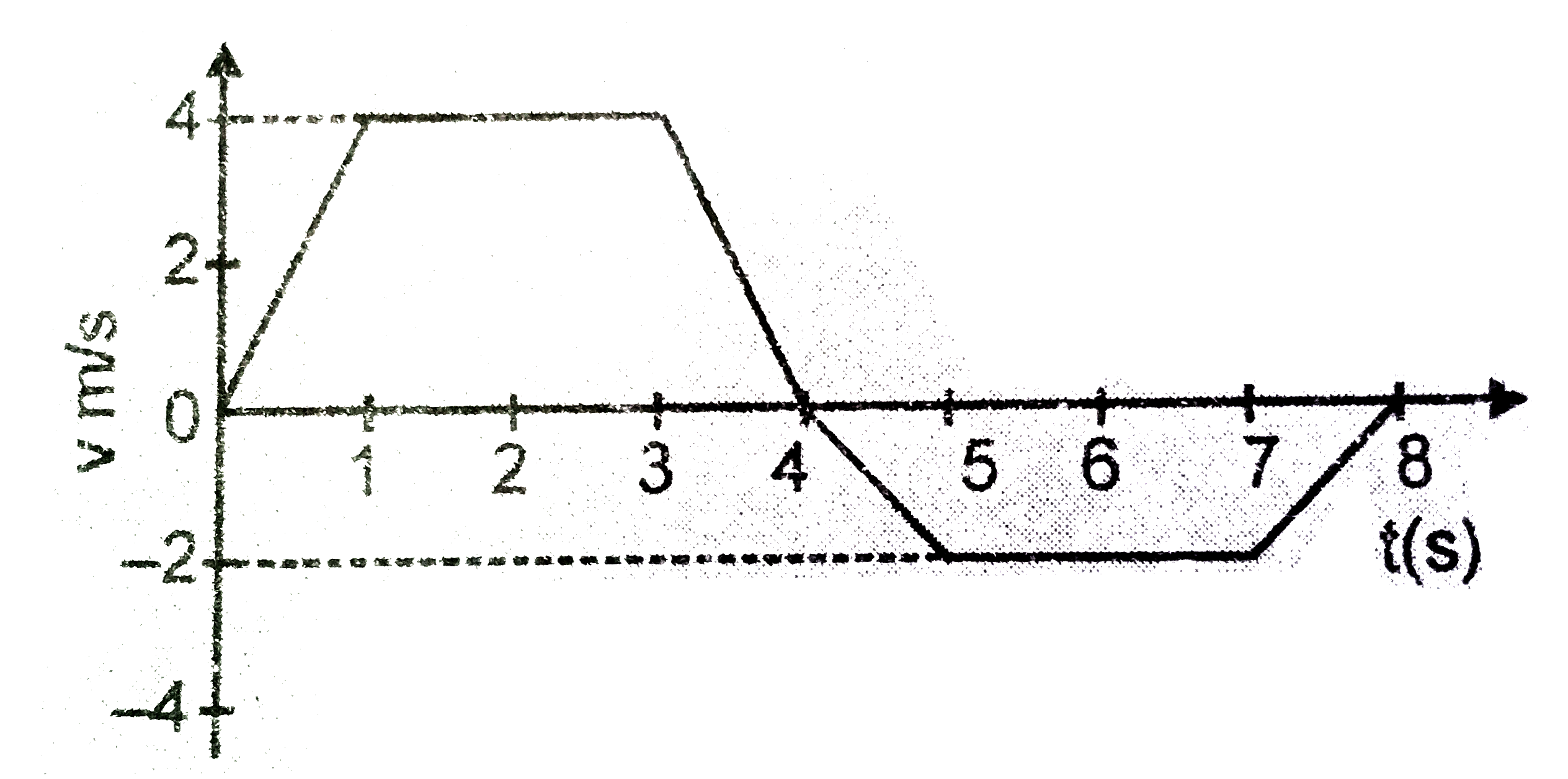 View Solution
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionThe position x of a particle varies with time t as x=at2−bt3.The acceleration of the particle will be zero at time t equal to
View SolutionThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
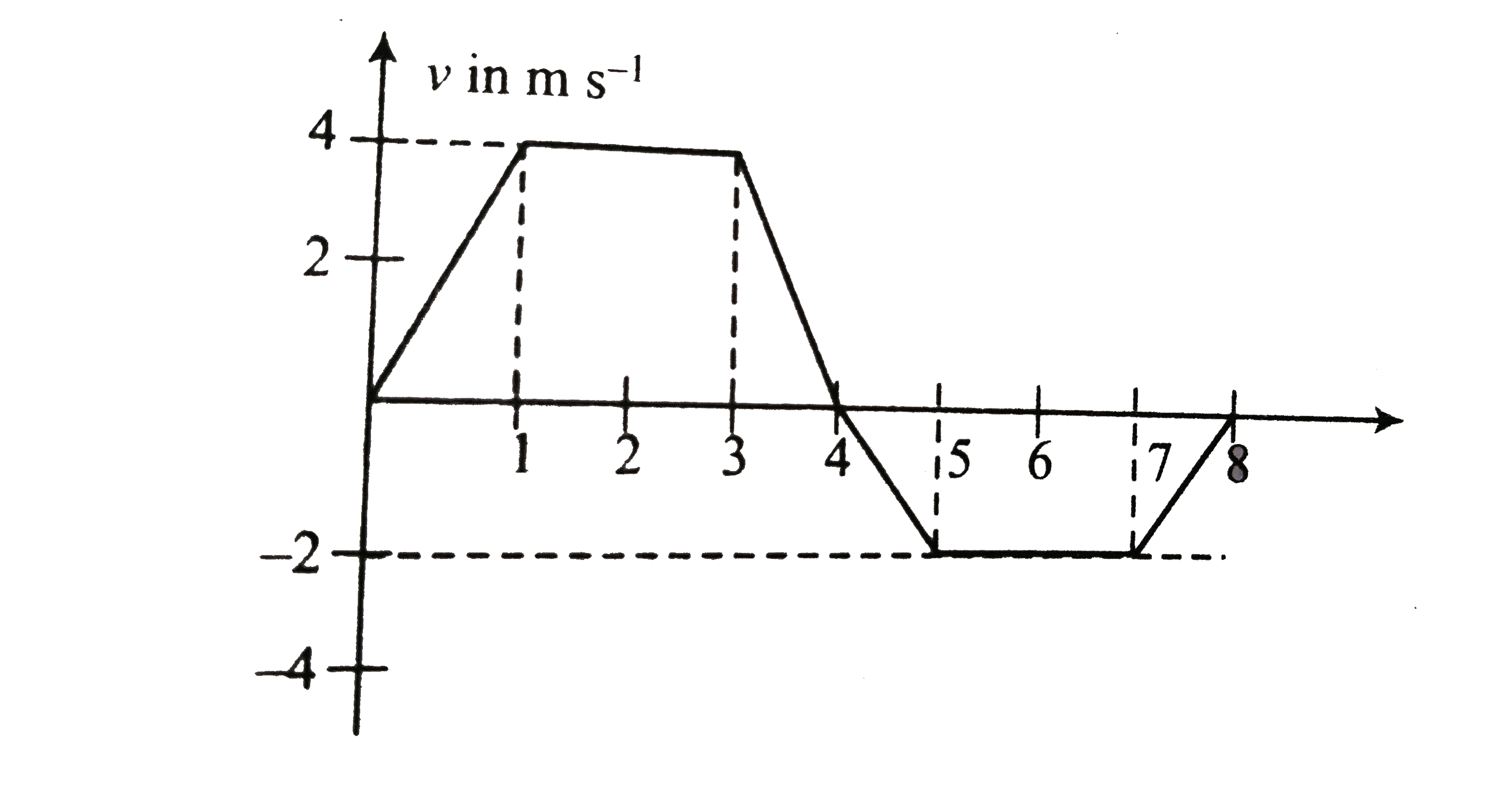 .
.
The distance of the particle from the origin after 8s is .View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View SolutionThe velocity time graph of a particle moving along a straight line is shown in the figure. In the time interval from t=0 to t=8 second, answer the following three question.

The distance travelled by the particle is :View Solution
