The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed asgainst ilt. A. Find the compression of the spring in the equilibrium position. b.The blocks are pushed a further distance (2k)(m1+m2)gsinθ against the spring and released. Find the position where the two blocks separate. c. What is the common speed of blocks at the time of separation?

The correct Answer is:→x=(m1+m2)gsinθk
x1=2k(m1+m2)gsinθ
v=√{3k(m1+m2)}gsinθ
a. At the equilibrium condition
kx=(m1+m2)gsinθ
→x=(m1+m2)gsinθk
b. x1=2k(m1+m2)gsinθ
given When the system is released it will start to make SHM.
where , ω=√km1+m2
when the blocks lose contact
p=0
So m2gsinθ=m2x2×km1+m2
→x2=(m1+m2)gsinθk
so the blocks will lose contact with each other when the springs attain its natural length.
c.Let the common speed attained you both the block be v
12(m1+m2)v2−0
=11k(x1+x2)2−(m1+m2)gsinθ(x+x1)
[x+x1=total compression]
→12(m1+m2)v2
=12k(3k)(m1+m2)gsinθ−(m1+m2)gsinθ−(x1+x2)
→12(m1_m2)v2=
12(m1+m2)gsinθ×(3k)(m1+m2)gsinθ<br>rarr v=√{3k(m1+m2)}gsinθ
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
In the fig shown, a block of mass M is attached to the spring and another block of mass 2M has been placed over it. The system is in equilibrium. The block are pushed down so that the spring compresses further by 9MgK. System is released
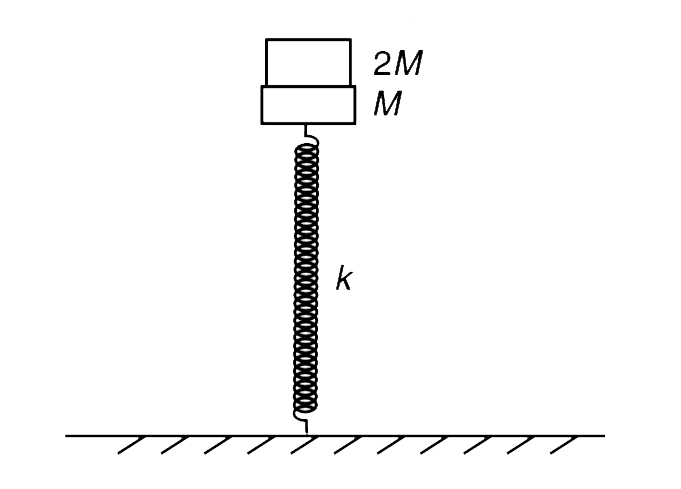
(a) At what height above the position of release, the block of mass 2M will lose contact with the other block? (b) What is maximum height attained by 2M above the point of release?
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View Solution
Knowledge Check
The system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10N/m.
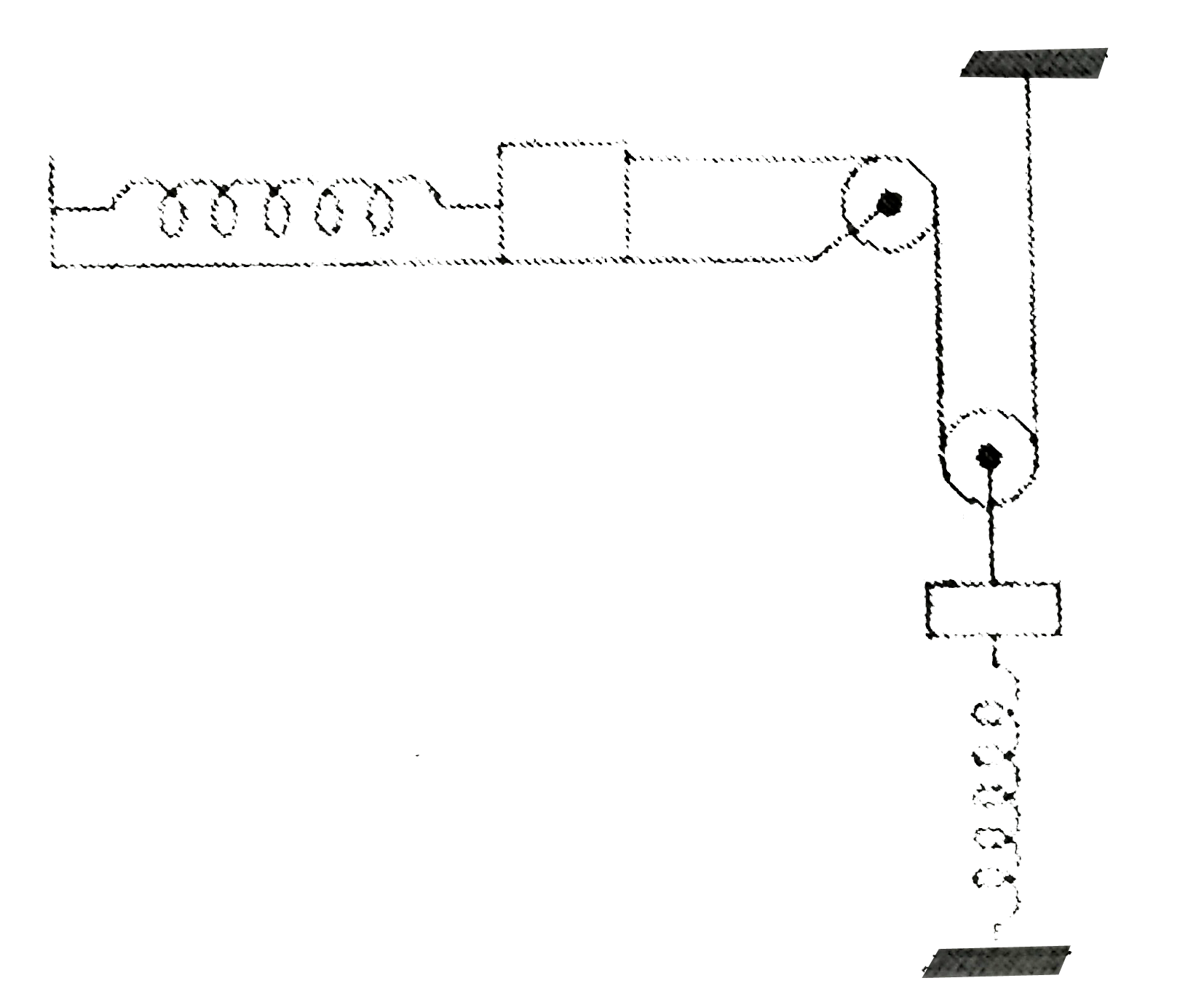
In the equilibrium position, speed of the block placed horizontally isA3.21m/sB2.21m/sC1.93m/sD1.26m/sTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
 A12π√k2MB12π√kMC12π√2kMD12π√Mk
A12π√k2MB12π√kMC12π√2kMD12π√MkIn the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A block of mass m moving at a speed v compresses as spring thrugh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m moving at a speed v compresses a spring throgh a distance x before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo blocks of masses m1 and m2 are attached to the lower end of a light vertical spring of force constant k. The upper end of the spring is fixed. When the system is in equilibrium, the lower block (m2) drops off. The other block (m1) will

View Solution
