
The diagram below shows a sinusoidal curve. The equation of the curve will be
y=10sin(16t+π4)cm
y=10sin(16t+π3)cm
y=10sin(16t−π4)cm
y=10cos(16t+π4)cm
The correct Answer is:C
Let T be the time period , then T2=5π64−π64=4π64
T=π8s
ω=2πT=2π(π8)=16rads
Also, A=10cm (from the graph) The equation of the sinusoidal wave can be written as y=10sin(16t+ϕ) cm where ϕ is the initial phase. From the graph, corresponding to the crest =10cm, when
t=3π64.
=10cm=10sin[16(3π64)+ϕ]cm
sin[3π4+ϕ]=1 or 3π4+ϕ=π2⇒ϕ=−π4
y=10sin(16t−π4)
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
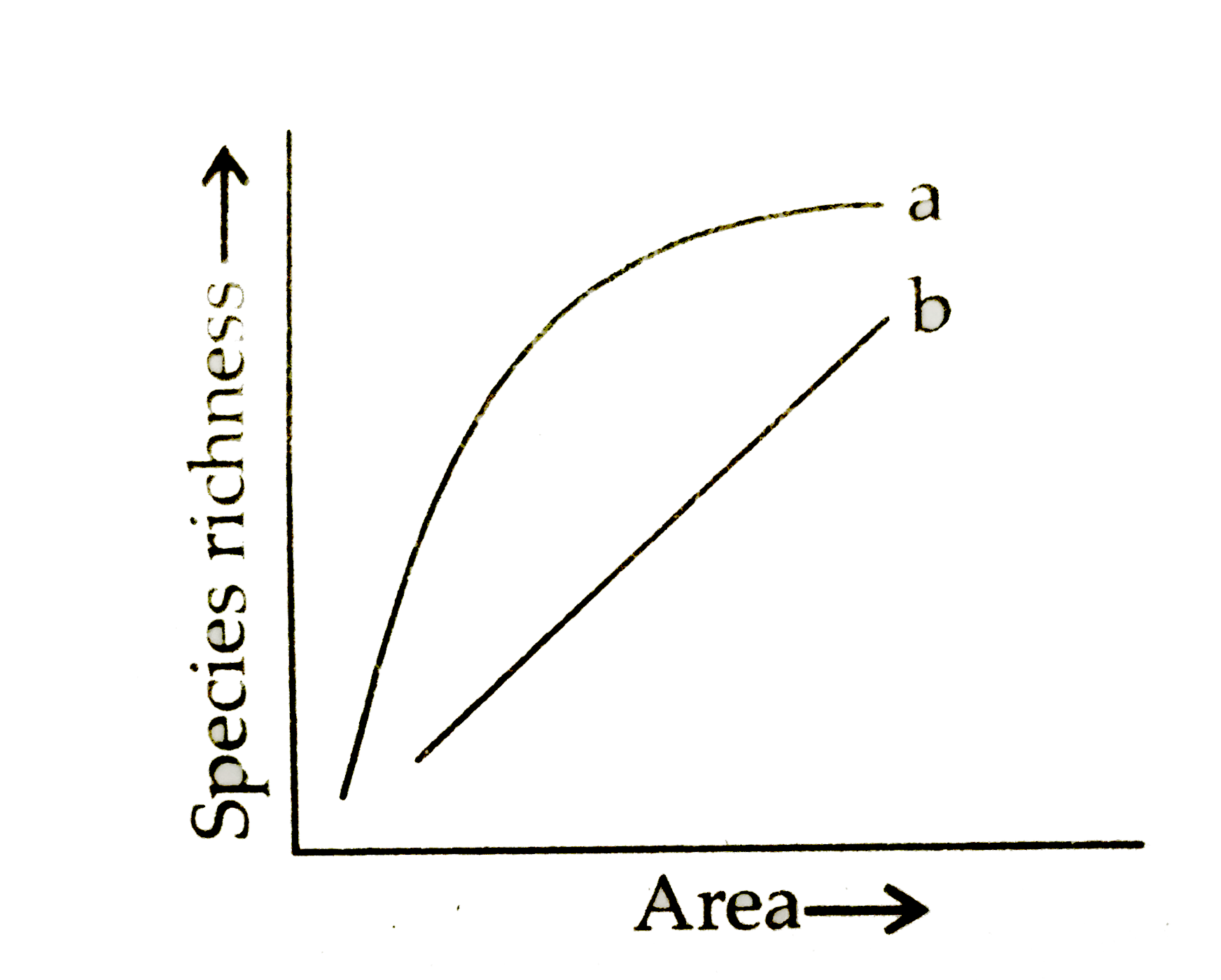
The above graph show Species-Area relationship. Write the equation of the curve a and explain.
View SolutionThe x-intercept of the tangent to a curve is equal to the ordinate of the point of contact. The equation of the curve through the point (1,1) is
View SolutionThe sum of the squares of the perpendicular drawn from the points (0,1) and (0,−1) to any tangent to a curve is 2. The equation of the curve, is
View SolutionA curve passes through the point (0,1) and the gradient at (x,y) on it is y(xy−1). The equation of the curve is
View SolutionA curve y=f(x) passes through point P(1,1) . The normal to the curve at P is a (y−1)+(x−1)=0 . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is
View SolutionFind the slope of normal to the curve if equation of the curve is y=x2+x−2 at (1,2)
View SolutionFind the slope of normal to the curve if equation of the curve is y2=4x at ( 4, 5)
View SolutionFind the slope of normal to the curve if equation of the curve is y2=4ax at (0 , 0)
View SolutionThe osciallations represented by curve 1 in the graph are expressed by equation x=Asinεt. The equation for the oscillations represented by curve 2 is expressed as

View Solution
The oscillations represented by curve 1 in the graph are expressed by equationx=Asinωt. The equation for the oscillation represented by curve 2 is expressed as
View Solution
