The ladder shown in the figure is light and stands on a frictionless horizontal surface. Arms AB and BC are of equal length and M and N are their mid points. Length of MN is half that of AB. A man of mass M is standing at the midpoint of BM. Find the tension in the mass less rod MN. Consider the man to be a point object.
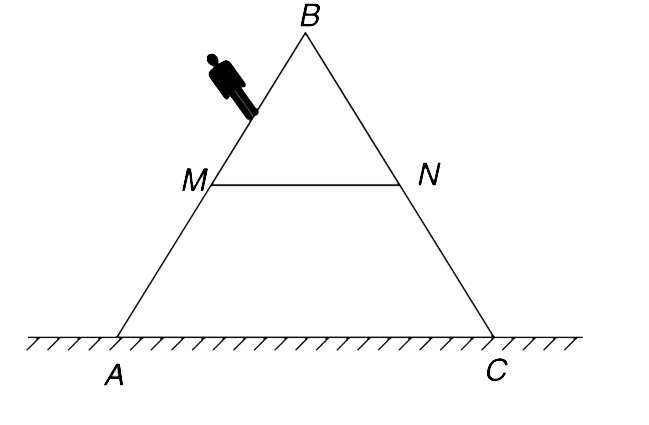
The correct Answer is:√34Mg
Topper's Solved these Questions
Similar Questions
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionIn ΔABC,M is the mid point of BC. Length of AM is 9, N is a point on AM such that MN=1. What is the distance of N from the centroid of the triangle?
View Solution
Knowledge Check
A uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is
 AFB3FC5F4D7F4
AFB3FC5F4D7F4
AB is a platform of length 10m kept on frictionless horizontal surface. A man of same mass is standing on end A. Friction coefficient between shoe of the man and platform is 0.5. Man starts running from A and stops at B. Find the minimum time (in seconds) required by the person to arrive at B.

View SolutionAB is a platform of length 10m kept on frictionless horizontal surface. A man of same mass is standing on end A. Friction coefficient between shoe of the man and platform is 0.5. Man starts running from A and stops at B. Find the minimum time (in seconds) required by the person to arrive at B.

View SolutionABCD is a regular tetrahedron. MandN are the mid points of the edges ABandCD. It the length of AB is a, then ∣∣¯¯¯¯¯¯¯¯MN∣∣2=
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View SolutionIn the adjoining figure
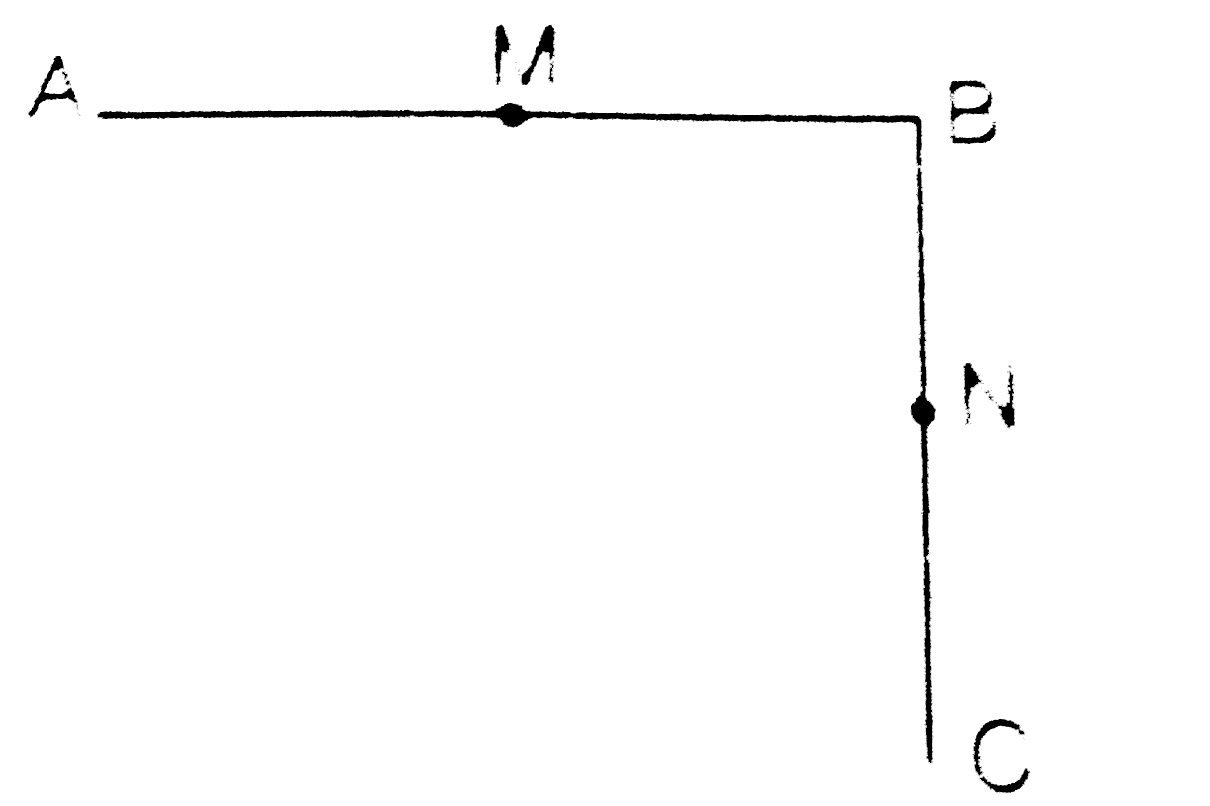
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View SolutionIn the adjoining figure

(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
View Solution
