The upper half of an inclined plane with inclination ϕ is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
μ=1tanθ
μ=2tanθ
μ=2tanθ
μ=tanθ
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of the body on the inclined plane, considering both the smooth and rough sections.
Step 1: Analyze the motion from the top to the bottom of the smooth section
1. Identify the parameters: The inclined plane has an angle of inclination ϕ. The upper half (length L/2) is smooth, and the lower half (also length L/2) is rough with a coefficient of friction μ.
2. Initial conditions: The body starts from rest, so the initial velocity U=0.
3. Acceleration on the smooth section: The acceleration a of the body while sliding down the smooth section is given by:
a=gsinϕ
4. Using the kinematic equation: We can find the maximum velocity Vmax at the bottom of the smooth section (point B) using the equation:
V2=U2+2aS
Substituting the values:
V2max=0+2(gsinϕ)(L/2)
Simplifying this gives:
V2max=gLsinϕ
Step 2: Analyze the motion from the bottom of the smooth section to the bottom of the rough section
1. For the rough section: The body starts with a velocity Vmax and will come to rest at the bottom (point C).
2. Net acceleration on the rough section: The net acceleration while moving down the rough section is:
anet=gsinϕ−μgcosϕ
3. Using the kinematic equation again: Since the final velocity at point C is zero, we can write:
0=V2max+2anetS
Substituting S=L/2 and anet:
0=gLsinϕ+2(gsinϕ−μgcosϕ)(L2)
Simplifying gives:
0=gLsinϕ+gLsinϕ−μgLcosϕ
0=2gLsinϕ−μgLcosϕ
Step 3: Solve for the coefficient of friction μ
1. Rearranging the equation:
μgLcosϕ=2gLsinϕ
Dividing both sides by gL (assuming gL≠0):
μcosϕ=2sinϕ
2. Solving for μ:
μ=2sinϕcosϕ=2tanϕ
Final Answer
The coefficient of friction μ for the lower half of the inclined plane is:
μ=2tanϕ
1. Identify the parameters: The inclined plane has an angle of inclination ϕ. The upper half (length L/2) is smooth, and the lower half (also length L/2) is rough with a coefficient of friction μ.
2. Initial conditions: The body starts from rest, so the initial velocity U=0.
3. Acceleration on the smooth section: The acceleration a of the body while sliding down the smooth section is given by:
a=gsinϕ
4. Using the kinematic equation: We can find the maximum velocity Vmax at the bottom of the smooth section (point B) using the equation:
V2=U2+2aS
Substituting the values:
V2max=0+2(gsinϕ)(L/2)
Simplifying this gives:
V2max=gLsinϕ
1. For the rough section: The body starts with a velocity Vmax and will come to rest at the bottom (point C).
2. Net acceleration on the rough section: The net acceleration while moving down the rough section is:
anet=gsinϕ−μgcosϕ
3. Using the kinematic equation again: Since the final velocity at point C is zero, we can write:
0=V2max+2anetS
Substituting S=L/2 and anet:
0=gLsinϕ+2(gsinϕ−μgcosϕ)(L2)
Simplifying gives:
0=gLsinϕ+gLsinϕ−μgLcosϕ
0=2gLsinϕ−μgLcosϕ
1. Rearranging the equation:
μgLcosϕ=2gLsinϕ
Dividing both sides by gL (assuming gL≠0):
μcosϕ=2sinϕ
2. Solving for μ:
μ=2sinϕcosϕ=2tanϕ
The coefficient of friction μ for the lower half of the inclined plane is:
μ=2tanϕ
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
The upper half of an inclined plane with an angle of inclination theta, is smooth while the lower half is rough. A body starting from rest at the top of the inclined plane comes to rest at the bottom of the inclined plane. Then the coefficient of friction for the lower half is
View SolutionThe upper portion of an inclined plane of inclination a is smooth and the lower portion is rough. A partical slide down from rest the top and just comes to rest at the foot . If the ratio of smooth length to rough length is m:n, find the coefficient of friction .
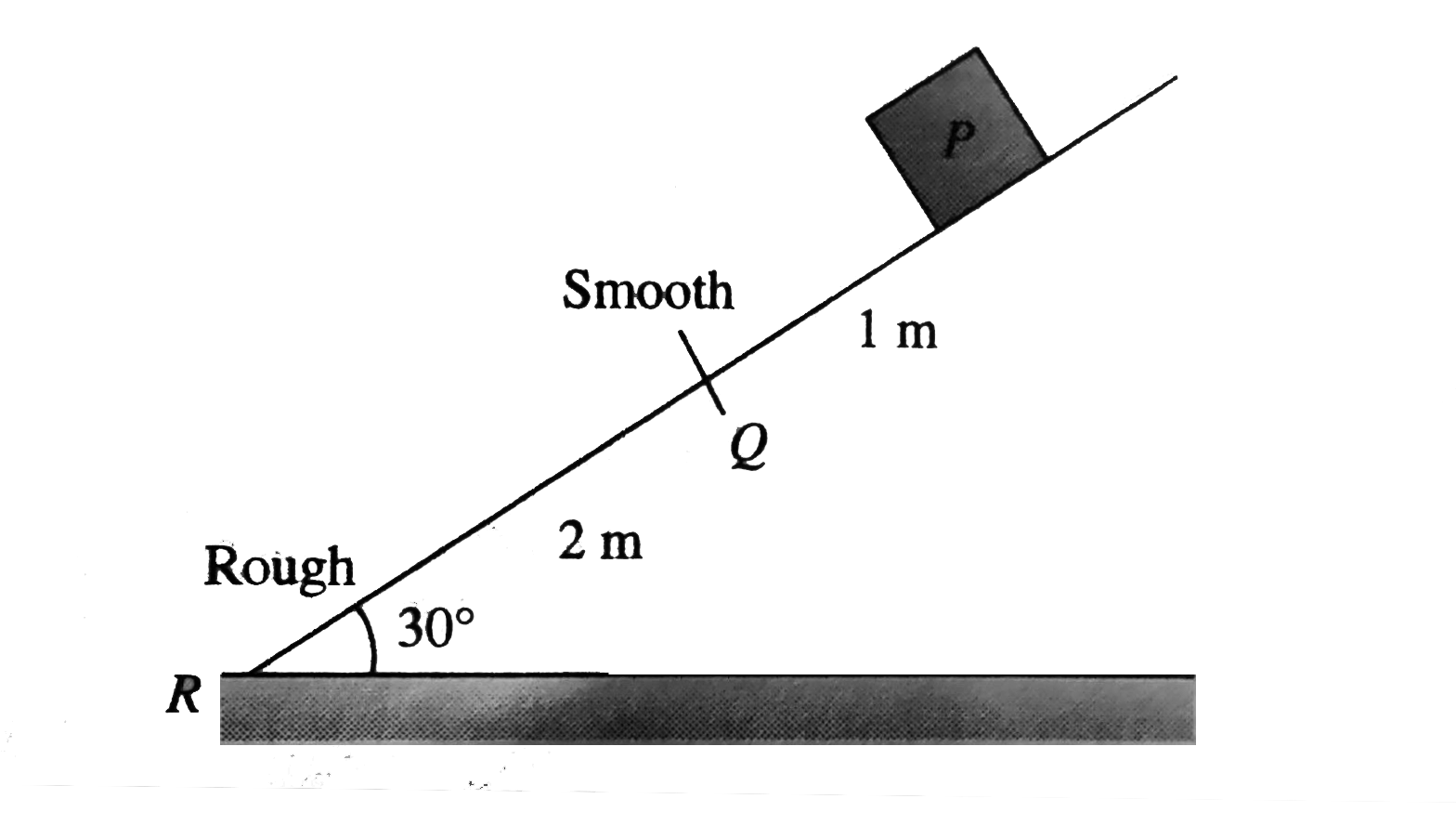
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
View SolutionA block of mass m is released on the top of a smooth inclined plane of length x and inclination θ as shown in figure. Horizontal surface is rough. If block comes to rest after moving a distabce d on the horizontal surface, then coefficient of friction between block and surface is :-
View SolutionA body weighing 20kg just slides down a rough inclined plane that rises 5 in 12. What is the coefficient of friction ?
View SolutionA weight w is to be moved from the bottom to the top of an inclined plane of inclination θ to the horizontal. If a smaller force is to be applied to drag it along the plane in comparison to lift it vertically up, the coefficient of friction should be such that.
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
View SolutionA block is pushed up a rough inclined plane of 45°. If the time of descent is twice the time of ascent, the coefficient of friction is
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View Solution
