Three solenoid coils of same dimension, same number of turns and same number of layers of windings are taken. Coil 1 with inductance L1 was would using a wire of resistance 11Ω/m, coil 2 with inductance L2 was wound using the similar wire but the direction of winding was reversed in each layer, coil 3 with inductance L3 was wound using a superconducting wire. The self-inductance of the coils L1,L2 and L3 are
L1=L2=L3
L1=L2,L3=0
l1=l3,l2=0
L1>L2>L3
The correct Answer is:B
To solve the problem regarding the self-inductance of three solenoid coils, we need to analyze the properties of each coil based on the information provided.
1. Understanding Inductance: The self-inductance L of a solenoid is given by the formula:
L=μ0n2All
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length,
- A is the cross-sectional area,
- l is the length of the solenoid.
2. Coil 1 (Inductance L1): This coil is wound with a wire of resistance 11Ω/m. The inductance L1 is determined by the number of turns and the physical dimensions of the coil. Since the dimensions and number of turns are the same as the other coils, we can denote:
L_1 = k \quad \text{(where k is a constant depending on geometry)}
3. Coil 2 (Inductance L2): This coil is wound with the same wire, but the direction of winding is reversed in each layer. The self-inductance depends on the number of turns and the geometry, not on the direction of winding. Therefore, the inductance remains the same:
L2=k
4. Coil 3 (Inductance L3): This coil is wound using a superconducting wire. In the case of superconductors, below the critical temperature, the resistance becomes zero, and the inductance can be considered to be zero as well because the current can flow indefinitely without any energy loss. Thus:
L3=0
5. Conclusion: From the above analysis, we can summarize the inductances:
- L1=k
- L2=k
- L3=0
Thus, we conclude that:
L1=L2andL3=0
Final Answer:
- L1=L2
- L3=0
L=μ0n2All
where:
- μ0 is the permeability of free space,
- n is the number of turns per unit length,
- A is the cross-sectional area,
- l is the length of the solenoid.
L_1 = k \quad \text{(where k is a constant depending on geometry)}
L2=k
L3=0
- L1=k
- L2=k
- L3=0
L1=L2andL3=0
- L1=L2
- L3=0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If 'N' is the number of turns in a coil, the value of self inductance varies as
AN0BNCN2DN−2 - Question 2 - Select One
If the number of turns per units length of a coils of solenoid is doubled , the self- inductance of the soleniod will
Aremain unchangedBbe halvedCbe doubledDbecome four times - Question 3 - Select One
If the self inductance of 500 turns coil is 125 mH, then the self inductance of the similar coil of 800 turns is
A48.8mHB200mHC290mHD320mH
The inductors of self inductance L1 and L2 are put in series .
View SolutionFigure shows a rectangular coil near a long wire. The mutual inductance of the combination is
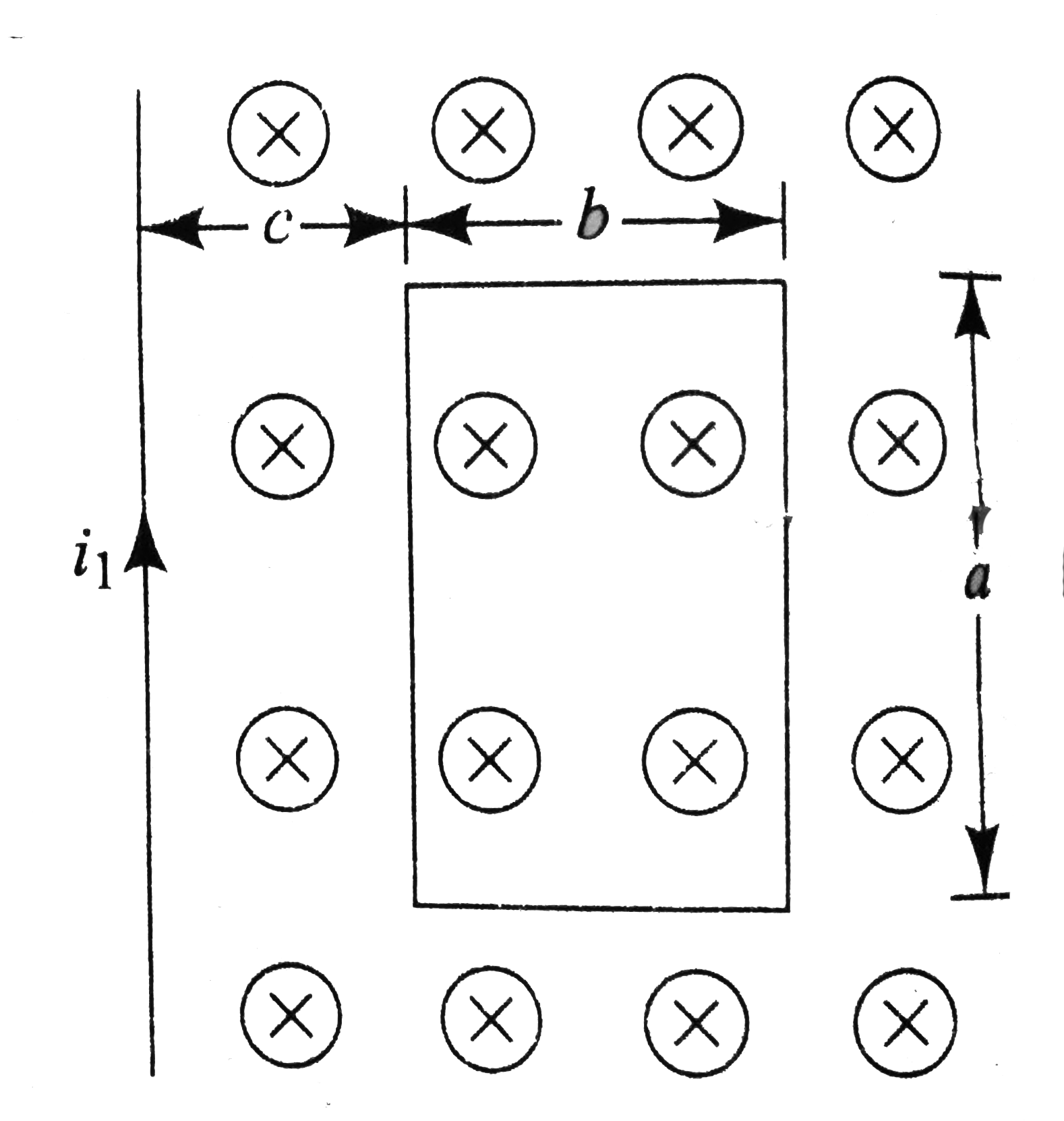 View Solution
View SolutionA coil of Cu wire (radius r, self-inductance L) is bent in two concentric turns each having radius r2. The self-inductance now
View SolutionDerive an expression for the total magnetic energy stored in two coils with inductances L1 and L2 and mutual inductance M, when the currents in the coils are I1 and I2, respectively.
View SolutionWhen the number of turns in a coil is doubled without any change in the length of the coil, its self-inductance becomes
View Solution

