Two blocks of equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constant force F. Find the tension in the string joining the blocks.
To solve the problem, we need to find the tension in the string connecting the two blocks when one of the blocks is pulled with a constant force F. Here’s a step-by-step solution:
Step 1: Understand the System
We have two blocks of equal mass m connected by a light string. One block is being pulled with a force F. Since the blocks are connected, they will have the same acceleration.
Step 2: Calculate the Total Mass
The total mass of the system (both blocks) is:
Total mass=m+m=2m
Step 3: Apply Newton's Second Law
According to Newton's second law, the net force acting on the system is equal to the total mass multiplied by the acceleration:
F=(2m)⋅a
where a is the acceleration of the system.
Step 4: Solve for Acceleration
Rearranging the equation gives us the acceleration of the system:
a=F2m
Step 5: Analyze Block A
Now, let’s analyze the forces acting on block A (the one being pulled). The only force acting on block A in the direction of motion is the tension T in the string. According to Newton's second law for block A:
T=m⋅a
Step 6: Substitute Acceleration
Substituting the value of a from Step 4 into the equation gives:
T=m⋅(F2m)
Step 7: Simplify the Equation
Simplifying this expression, we find:
T=F2
Conclusion
Thus, the tension in the string joining the two blocks is:
F2
We have two blocks of equal mass m connected by a light string. One block is being pulled with a force F. Since the blocks are connected, they will have the same acceleration.
The total mass of the system (both blocks) is:
Total mass=m+m=2m
According to Newton's second law, the net force acting on the system is equal to the total mass multiplied by the acceleration:
F=(2m)⋅a
where a is the acceleration of the system.
Rearranging the equation gives us the acceleration of the system:
a=F2m
Now, let’s analyze the forces acting on block A (the one being pulled). The only force acting on block A in the direction of motion is the tension T in the string. According to Newton's second law for block A:
T=m⋅a
Substituting the value of a from Step 4 into the equation gives:
T=m⋅(F2m)
Simplifying this expression, we find:
T=F2
Thus, the tension in the string joining the two blocks is:
F2
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer17videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -29videos
NEWTON'S LAWS OF MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions64videos
LAWS OF THERMODYNAMICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
Similar Questions
The block of mass m is at rest. Find the tension in the string A .
 View Solution
View SolutionTwo identical blocks A and B each of mass M are connected to each other through a light string. The system is placed on a smooth horizontal floor. When a constant force F is applied horizontally on the block A, find the tension in the string.
View SolutionA block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View Solution
Find out the acceleration of the blocks and tensions in the strings.View SolutionA block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20J in 1s.
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
 View Solution
View SolutionA block of mass 10 kg is hanging over a smooth and light pulley through a light string and the other end of the string is pulled down by a constant force F. The kinetic energy of the block increases by 20 J in 1 s
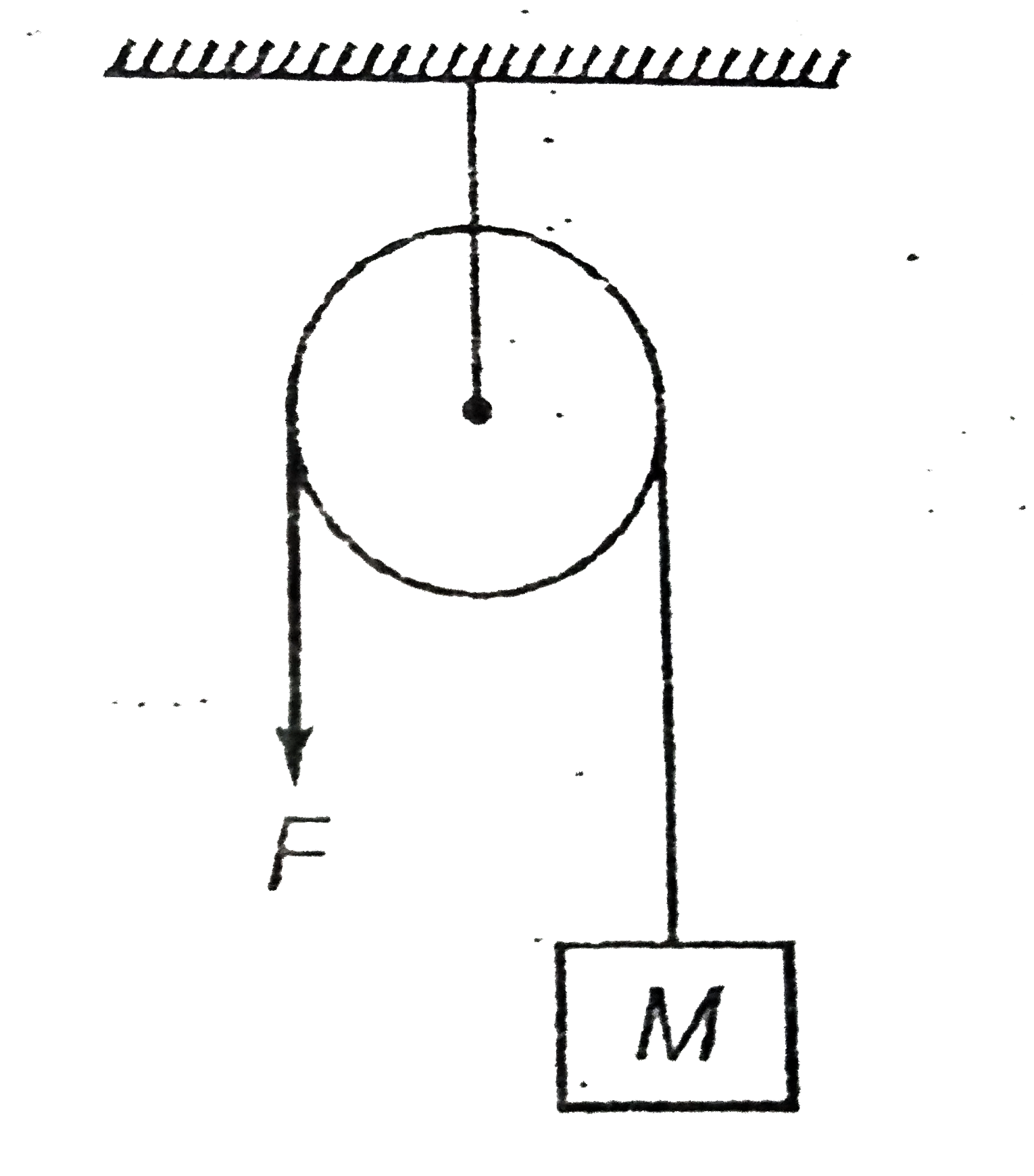 View Solution
View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.
 View Solution
View SolutionTwo block of masses m1andm2 are lying on a frictionless horizontal table connected by a light string m2 is pulled by horizontal force F. Calculate the tension in the string .
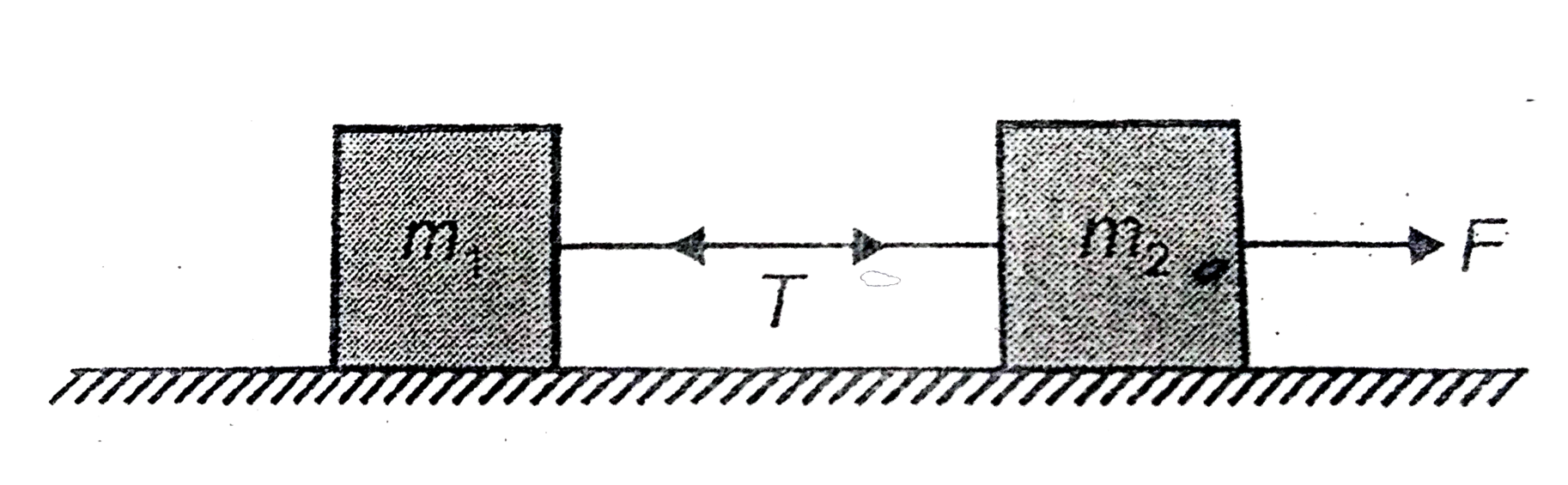 View Solution
View SolutionA block of mass M hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic of the block increases by 40J in 1s. State whether the following statements are true or false.
(a) The tension in the string is Mg .
(b) The work done the tension on the block is 40J.
(c) the tension in the string is F.
(d) The work done by the force of gravity is 40J in the above 1s .View Solution
