Two concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
To solve the problem of finding the change in electric potential on the outer shell when two concentric spherical conducting shells are connected by a conducting wire, we can follow these steps:
1. Identify the Charges and Radii:
- Let the inner spherical shell (S1) have a radius R and charge Q.
- Let the outer spherical shell (S2) have a radius 2R and charge 2Q.
2. Calculate the Initial Electric Potential:
- The electric potential V at the surface of a conducting sphere is given by the formula:
V=kQr
- For the inner shell (S1):
V1=kQR
- For the outer shell (S2):
V2=k2Q2R=kQR
3. Determine the Initial Potentials:
- The potential on the inner shell (S1) is:
V1=kQR
- The potential on the outer shell (S2) is:
V2=kQR
4. Connect the Shells with a Wire:
- When the two shells are connected by a conducting wire, charge will flow from the higher potential to the lower potential until they reach the same potential.
- Since both potentials are equal initially, we need to consider the total charge after connection.
5. Calculate the Total Charge:
- The total charge after connecting the shells is:
Qtotal=Q+2Q=3Q
6. Final Charge Distribution:
- After connecting, the charge will redistribute such that both shells have the same potential.
- Let the final charge on the inner shell be q1 and on the outer shell q2.
- We have:
q1+q2=3Q
7. Final Potential Calculation:
- The potential on the outer shell (S2) after redistribution is:
V2,final=kq22R
- Since both shells must have the same potential:
V1,final=V2,final
- Therefore:
kq1R=kq22R
- This simplifies to:
2q1=q2
8. Substituting for Charges:
- From q1+q2=3Q and 2q1=q2:
q1+2q1=3Q⟹3q1=3Q⟹q1=Q
- Thus, q2=2Q.
9. Final Potentials:
- The final potential on the outer shell (S2) is:
V2,final=k2Q2R=kQR
10. Calculate Change in Potential:
- The initial potential on the outer shell was kQR and the final potential is also kQR.
- Therefore, the change in potential ΔV on the outer shell is:
ΔV=V2,final−V2,initial=kQR−kQR=0
Final Answer:
The change in electric potential on the outer shell when both are connected by a conducting wire is ΔV=0.
- Let the inner spherical shell (S1) have a radius R and charge Q.
- Let the outer spherical shell (S2) have a radius 2R and charge 2Q.
- The electric potential V at the surface of a conducting sphere is given by the formula:
V=kQr
- For the inner shell (S1):
V1=kQR
- For the outer shell (S2):
V2=k2Q2R=kQR
- The potential on the inner shell (S1) is:
V1=kQR
- The potential on the outer shell (S2) is:
V2=kQR
- When the two shells are connected by a conducting wire, charge will flow from the higher potential to the lower potential until they reach the same potential.
- Since both potentials are equal initially, we need to consider the total charge after connection.
- The total charge after connecting the shells is:
Qtotal=Q+2Q=3Q
- After connecting, the charge will redistribute such that both shells have the same potential.
- Let the final charge on the inner shell be q1 and on the outer shell q2.
- We have:
q1+q2=3Q
- The potential on the outer shell (S2) after redistribution is:
V2,final=kq22R
- Since both shells must have the same potential:
V1,final=V2,final
- Therefore:
kq1R=kq22R
- This simplifies to:
2q1=q2
- From q1+q2=3Q and 2q1=q2:
q1+2q1=3Q⟹3q1=3Q⟹q1=Q
- Thus, q2=2Q.
- The final potential on the outer shell (S2) is:
V2,final=k2Q2R=kQR
- The initial potential on the outer shell was kQR and the final potential is also kQR.
- Therefore, the change in potential ΔV on the outer shell is:
ΔV=V2,final−V2,initial=kQR−kQR=0
The change in electric potential on the outer shell when both are connected by a conducting wire is ΔV=0.
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False Type
5 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Two concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
View SolutionThree concentric conducting spherical shells of radii R, R2 and 3R carry charges Q,-2Q and 3Q, respectively compute the electric field at r=52R

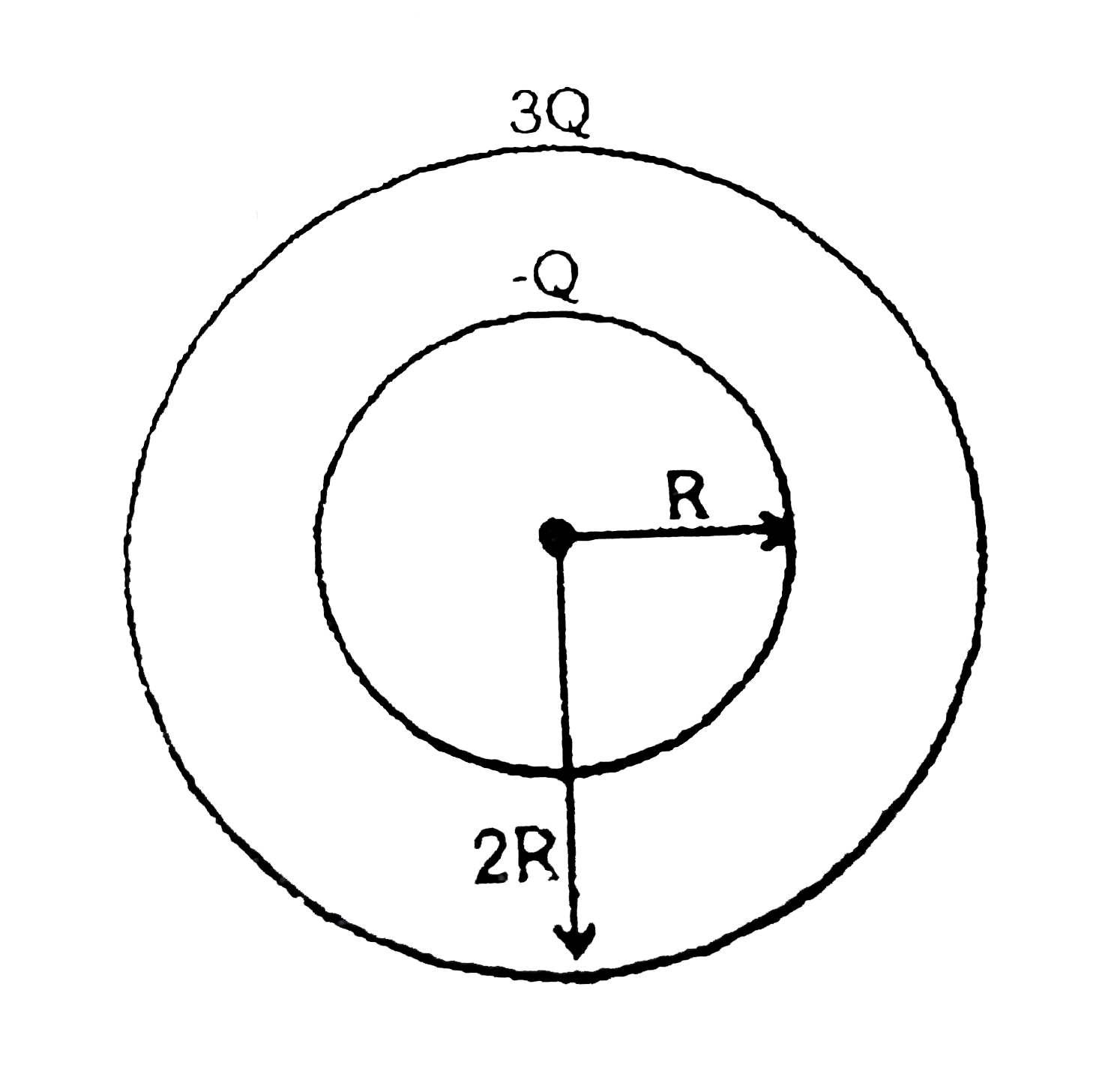
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
View SolutionThree concentric conducting spherical shells of radii R,2R carry charges Q, -2Q and 3Q, respectively. Find the electric potential at r = R and at r = 3 R, where r is the radii distance from the centre.

View SolutionTwo concentric spherical conducting shells of radii 'a' and 2a are initially given charges +2Q and +Q respectively as shown. The total heat dissipated after switch 'S' has been closed is (where k=14πε0)

View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View SolutionTwo concentric spherical shells of radii R and 2R have charges Q and 2Q as shown in figure

Choose the correct optin (K=14πε0)
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
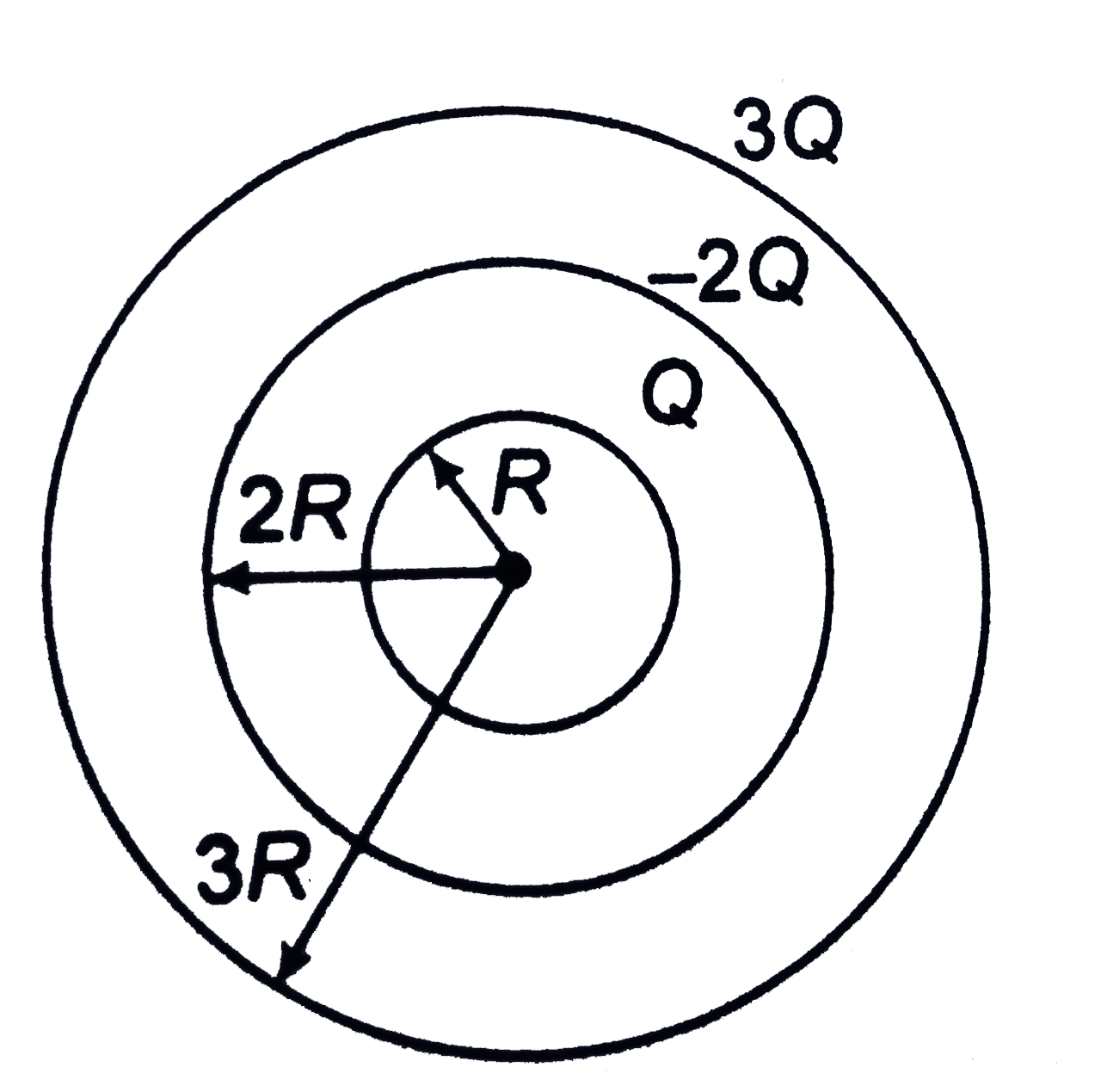
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre . b. Compute the electric field at r=52R
c. Compute the total electrostatic energy stored in the system.
The inner shell is now connected to the external one by a conducting wire, passing through a very small hole in the middle shell.
d. Compute the charges on the spheres of radii R and 3R.
e. Compute the electric field at r=52R
View Solution
