Two rods and are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are and and thermal conductivities and . The rate of heat transmission in the two rods will be equal, if
The correct Answer is:B
To solve the problem, we need to determine the condition under which the rate of heat transmission through two rods A and B is equal. We will use the formula for heat conduction, which is derived from Fourier's law of heat conduction.
1. Understand the Heat Transfer Formula:
The rate of heat transfer (I) through a rod can be expressed as:
I=ΔTR
where ΔT is the temperature difference across the rod and R is the thermal resistance.
2. Define Thermal Resistance:
The thermal resistance R for a rod can be given by:
R=LK⋅A
where:
- L is the length of the rod,
- K is the thermal conductivity of the material,
- A is the cross-sectional area of the rod.
3. Set Up the Equations for Both Rods:
For rod A:
R1=LK1⋅A1
For rod B:
R2=LK2⋅A2
4. Equate the Rates of Heat Transfer:
Since the ends of both rods are kept at the same temperature, the rate of heat transfer through both rods is equal:
IA=IB
This implies:
ΔTR1=ΔTR2
5. Cancel Out the Temperature Difference:
Since ΔT is the same for both rods, we can cancel it out:
R1=R2
6. Substituting the Resistance Values:
Substituting the expressions for R1 and R2:
LK1⋅A1=LK2⋅A2
7. Cancel the Lengths:
Since the lengths L are equal and non-zero, we can cancel L from both sides:
1K1⋅A1=1K2⋅A2
8. Cross Multiply:
Cross multiplying gives us:
K1⋅A1=K2⋅A2
Conclusion:
The rate of heat transmission in the two rods will be equal if:
K1⋅A1=K2⋅A2
The rate of heat transfer (I) through a rod can be expressed as:
I=ΔTR
where ΔT is the temperature difference across the rod and R is the thermal resistance.
The thermal resistance R for a rod can be given by:
R=LK⋅A
where:
- L is the length of the rod,
- K is the thermal conductivity of the material,
- A is the cross-sectional area of the rod.
For rod A:
R1=LK1⋅A1
For rod B:
R2=LK2⋅A2
Since the ends of both rods are kept at the same temperature, the rate of heat transfer through both rods is equal:
IA=IB
This implies:
ΔTR1=ΔTR2
Since ΔT is the same for both rods, we can cancel it out:
R1=R2
Substituting the expressions for R1 and R2:
LK1⋅A1=LK2⋅A2
Since the lengths L are equal and non-zero, we can cancel L from both sides:
1K1⋅A1=1K2⋅A2
Cross multiplying gives us:
K1⋅A1=K2⋅A2
The rate of heat transmission in the two rods will be equal if:
K1⋅A1=K2⋅A2
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
51 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check point 16.2
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
A composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivities K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
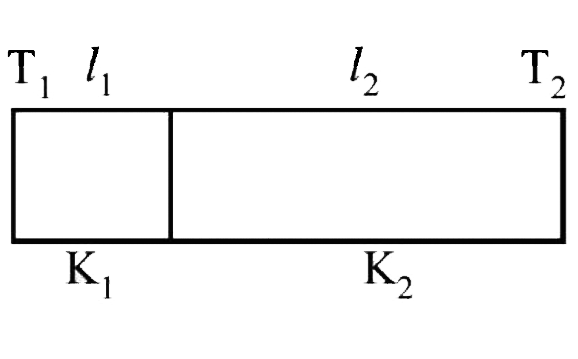
View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionTwo metal rods 1 and 2 of the same length have same temperature difference between their ends. Their thermal conductivities are K1andK2 and cross-section areas A1andA2 respectively. What is the required condition for the same rate of heat conduction in them?
View SolutionConsider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View SolutionTwo rods A and B are of equal length. Each rod has its ends at temperatures T1andT2. What is the condition that will ensure equal rate of flow of heat through the rods A and B ?
View SolutionTwo rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
View Solution
