Two small spheres are attached to the ends of a long light nonconducting rod at a distance 40 mm from each other. All three spheres are nonconducting, have identical masses m=1g, and a positive charge q=1C is distributed evenly on the surface of each sphere. The whole system is placed on a horizontal frictionless nonconducting surface. Initially, all three spheres are at rest and the middle sphere is located a distance 30 mm from one of the ends of the rod and a distance 10 mm from the other. Find the maximum speed v (∈ms−1) of the middle sphere after the system is released.
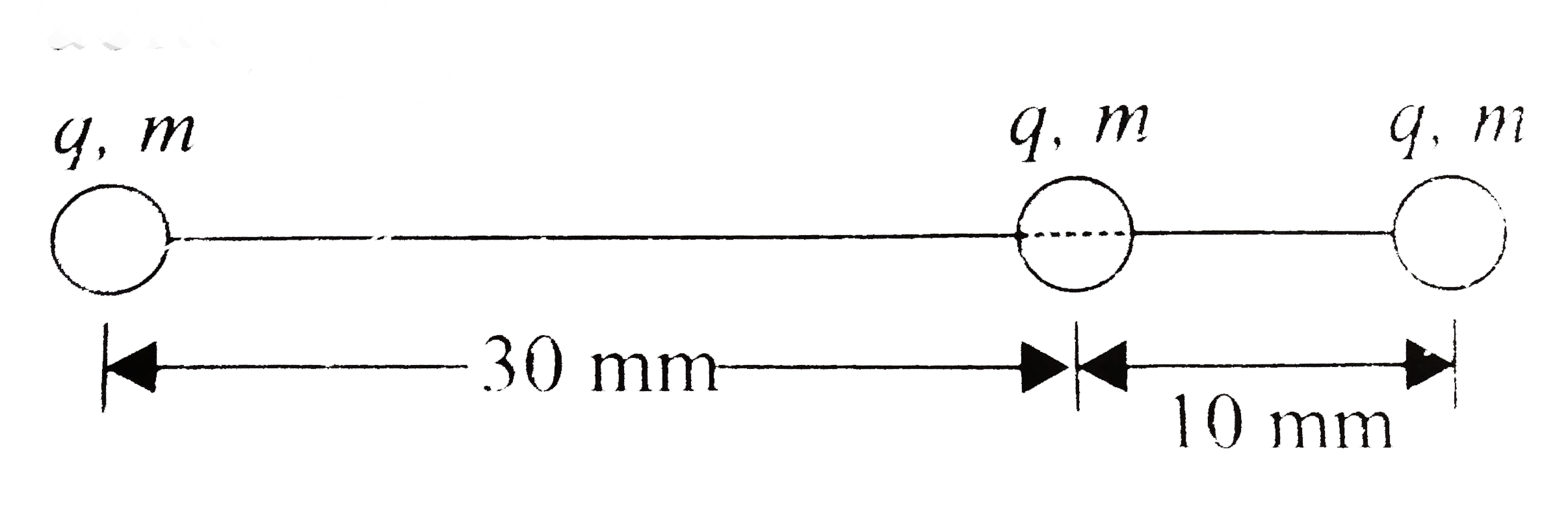

Since the charge is evely distributed, the charges can be treated as point charges. Looking at the "believe" and "after" pictures and taking right as positive and left as negative, conservation of momentum gives ∑→Pb=∑→Pa
0=2mv2−mv1,which gives v2=V1/2
The maximum velocity of the middle charge will occur when the middle charge is at the middle. Beyond the middle point, there will be a net force to the right that will tend to slow the charge down. The situation will be the same for the middle charge even if the two end charges are moving. Applying the law of conservation of energy to the system and using the middle charge position of maximum velocity as the "after" position, one gets Eb=Ea
PEb=KE+PEa
or kq23d+kq2d=12mv21+12(2m)v22+2kq22d
Now using the conservation of momentum result above for v2 and simplifying, we get
or kq23d=12mv21+mv214=3mv214
Finally solving for the maximum velocity
v1=2q3√kmd=20ms−1
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Fill in the blanks
10 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False Type
5 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
A charge q is distributed uniformly on the surface of a sold sphere of radius R. It covered by a concentric hollow conduction sphere of radius 2R. Find the charges inner and outer surface of hollow sphere if it is earthed.

View SolutionThree identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View SolutionTwo identical spherical masses are kept at some distance. Potential energy when a mass m is taken from the surface of one sphere to the other
View SolutionFour identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionA charge q is to be distributed on two conducting spheres. What should be the value of the charges on the spheres so that the repulsive force between them is maximum when they are placed at a fixed distance from each other in air ?
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA positive charge q is placed in a spherical cavity made in a positively charged sphere. The centres of sphere and cavity are displaced by a small distance →l. Force on charge q is :
View SolutionThere are three concentric conducting spherical shells. All of them are charged. The innermost sphere is connected by a conducting wire to the outermost sphere. Prove that the final charge on the innermost sphere is independent of the initial charge of outermost sphere.
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View Solution