Two spheres A and B of radius 'a' and 'b' respectively are at same electric potential. The ratio of the surface charge densities of A and B is
ab
ba
a2b2
b2a2
The correct Answer is:B
To solve the problem of finding the ratio of the surface charge densities of two spheres A and B that are at the same electric potential, we can follow these steps:
Step 1: Understand the Electric Potential of a Sphere
The electric potential V of a charged sphere with radius r and total charge Q is given by the formula:
V=KQr
where K is the electrostatic constant.
Step 2: Relate Charge to Surface Charge Density
The surface charge density σ is defined as the charge per unit area. For a sphere, the total charge Q can be expressed as:
Q=σ×Area=σ×4πr2
Thus, substituting this into the potential formula gives:
V=K(σ×4πr2)r=4πKσr1
Step 3: Express Potential in Terms of Surface Charge Density
For sphere A with radius a and surface charge density σA:
VA=4πKσAa1
For sphere B with radius b and surface charge density σB:
VB=4πKσBb1
Step 4: Set the Potentials Equal
Since both spheres are at the same electric potential:
VA=VB
This leads to:
4πKσAa1=4πKσBb1
Step 5: Simplify the Equation
We can cancel 4πK from both sides:
σAa=σBb
Step 6: Find the Ratio of Surface Charge Densities
Rearranging the equation gives:
σAσB=ba
Conclusion
Thus, the ratio of the surface charge densities of spheres A and B is:
σAσB=ba
Final Answer
The ratio of the surface charge densities of spheres A and B is ba.
---
The electric potential V of a charged sphere with radius r and total charge Q is given by the formula:
V=KQr
where K is the electrostatic constant.
The surface charge density σ is defined as the charge per unit area. For a sphere, the total charge Q can be expressed as:
Q=σ×Area=σ×4πr2
Thus, substituting this into the potential formula gives:
V=K(σ×4πr2)r=4πKσr1
For sphere A with radius a and surface charge density σA:
VA=4πKσAa1
For sphere B with radius b and surface charge density σB:
VB=4πKσBb1
Since both spheres are at the same electric potential:
VA=VB
This leads to:
4πKσAa1=4πKσBb1
We can cancel 4πK from both sides:
σAa=σBb
Rearranging the equation gives:
σAσB=ba
Thus, the ratio of the surface charge densities of spheres A and B is:
σAσB=ba
The ratio of the surface charge densities of spheres A and B is ba.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two conducting concentric, hollow spheres A and B have radii a and b respectively, with A inside B. Their common potentials is V. A is now given some charge such that its potential becomes zero. The potential of B will now be
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View Solution
Knowledge Check
Two spheres of radius a and b respectively are charged and joined by a wire. The ratio of electric field of the spheres is
AabBbaCa2b2Db2a2
Three plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is
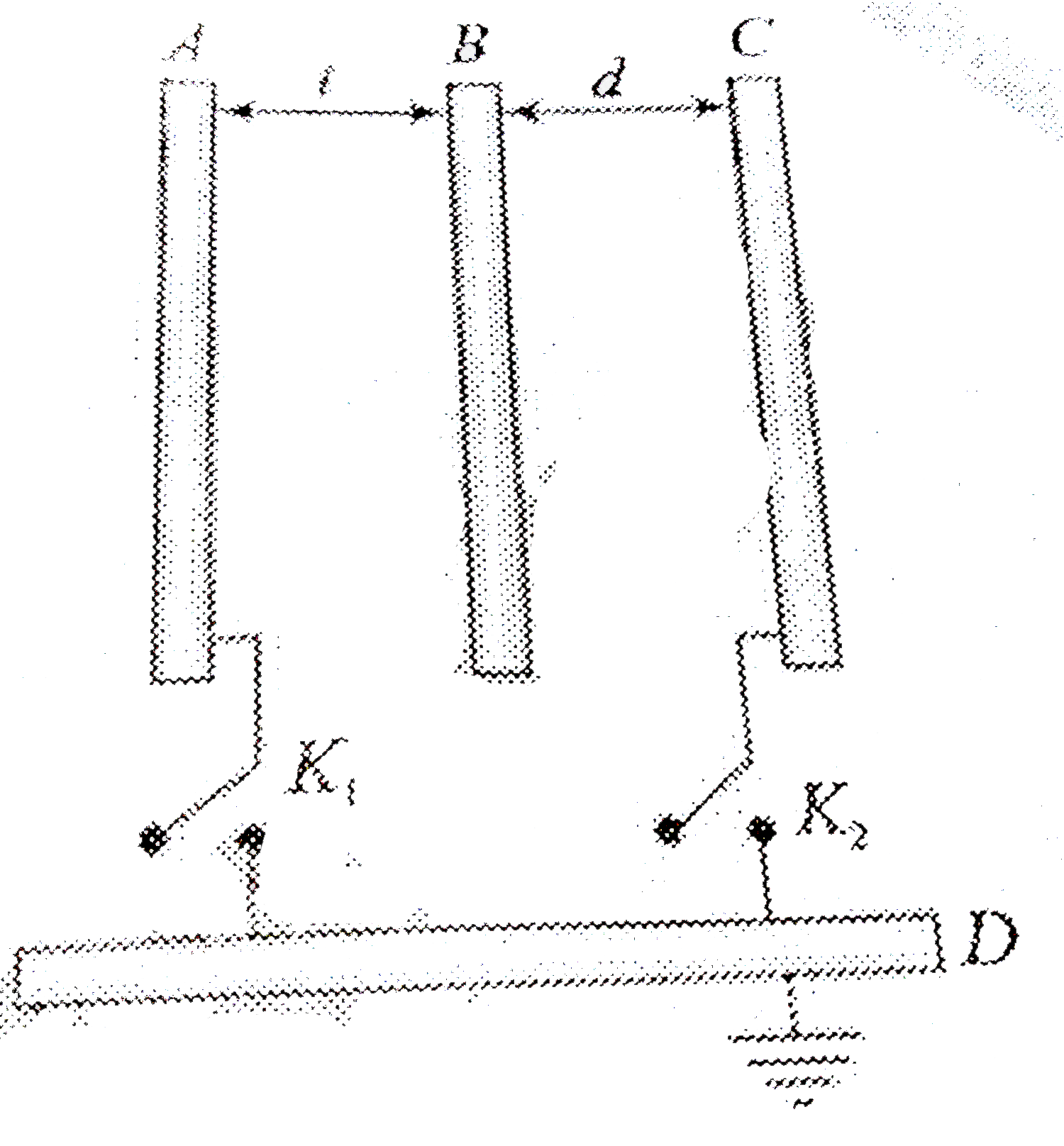
View SolutionA number of spherical conductors of different radius have same potential. Then the surface charge density on them.
View SolutionTwo metal spheres A and B of radii a & b (a < b) respectively are at a large distance apart. Each sphere carries a charge of 100μO. the sphere are connected by a conducting wire, then
View SolutionTwo isolated charged conducting spheres of radii a and b produce the same electric field near their surface. The ratio of electric potentials on their surfaces is
View SolutionTwo spheres of radii 2 cm and 3 cm are charged to the same potential. If σ and σ2 be respectively the values of surface charge density on the conductors, then the ratio σ1σ2 will be
View SolutionTwo spherical conductors A and B of radii R and 2R respectively , are separated by a large distance . If some charge is given to both the spheres and later they are connected by a conducting wire , then in equilibrium condition , the ratio of the magnitude of the electric fields at the surface of spheres A and B is
View Solution(i) Two isolated metal spheres A and B have radii R and 2R respectively and same charge q. Find which of the two spheres have
(a) greater capacitance
(b) greater energy density just outside the surface of the spheres.
(ii) (a) Show that the equipotential surfaces are closed together in the regions of strong field and far apart in the region of weak field. Draw equipotential surfaces for an electric dipole.
(b) Concentric equipotential surfaces due to a charged body placed at the centre are shown. Identify the polarity of the charge and draw the electric field lines due to it.
View Solution
