Two spherical bodies of mass $m_{1}$ and $m_{2}$ fall freely through a distance $h$ . before the body $m_{2}$ collides with the ground. If the coefficient of restitution of all collisions is $e$ , find the velocity of $m_{1}$ just after it collides with $m_{2}$

Video Solution

Text Solution

Verified by Experts

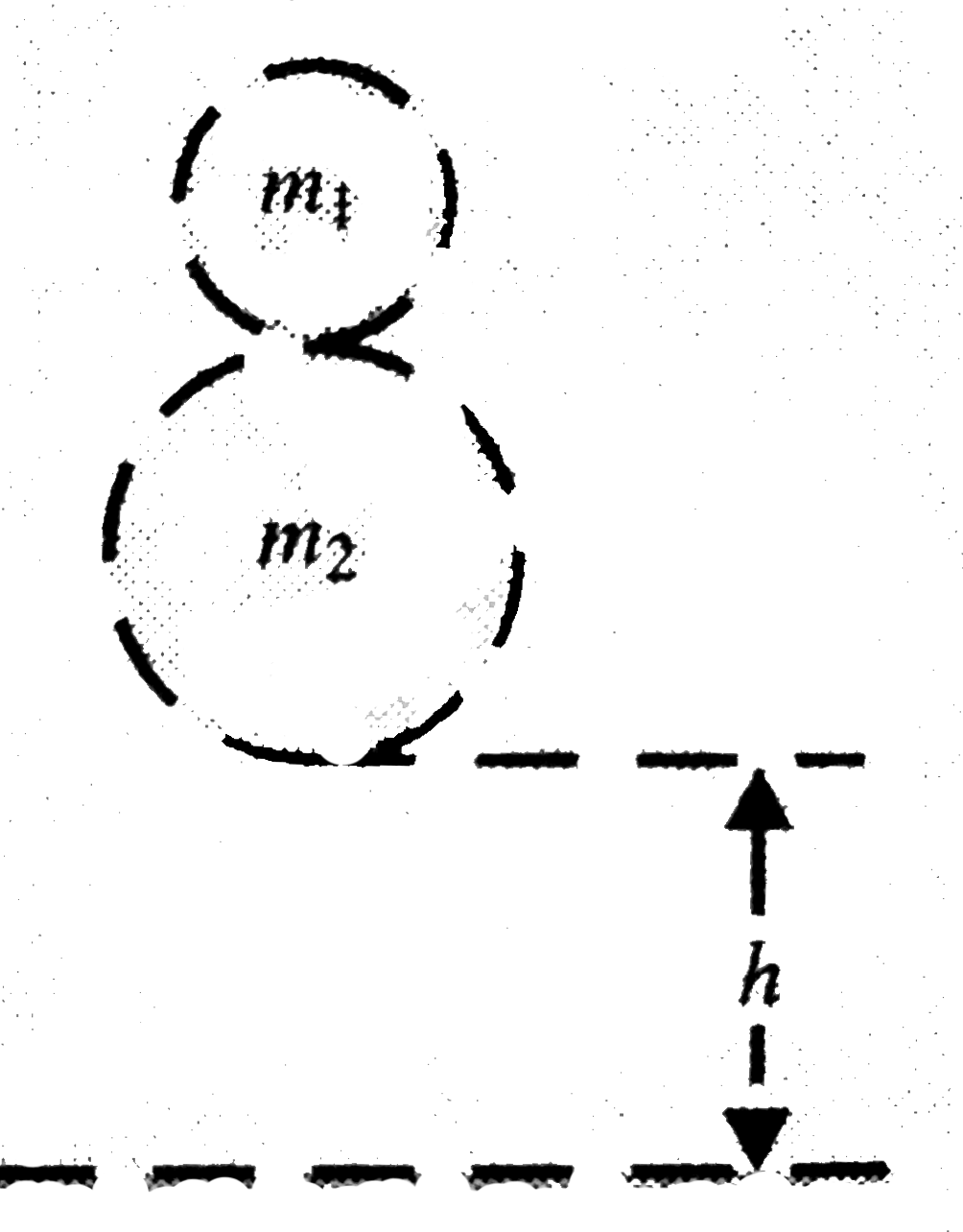
As the bodies $m_{1}$ and $m_{2}$ fall freely through a distance $h$ , $m_{2}$ collides with ground with velocity $v_{0} = \sqrt{2 g h}$ . Hence $m_{2}$ bounces up with a velocity $e v_{0}$ just after the collision with the ground.
Hence $m_{2}$ bounces up with a velocity $e v_{0}$ just after the collision with the ground. then it collides with the freely falling body $m_{1}$ . Just after the collision, let us assume that $v_{1}$ and $v_{2}$ are the velocities of $m_{1}$ and $m_{2}$ respectively.
ignoring the impulses due to the weights of the bodies during the period of collision. Let us conserve the momentum of the system $(m_{1} + m_{2})$ .
Conservation of linear momentum
$P = - m_{1} v_{0} + m_{2} e v_{0} = m_{1} v_{1} + m_{2} v_{2}$ .......i

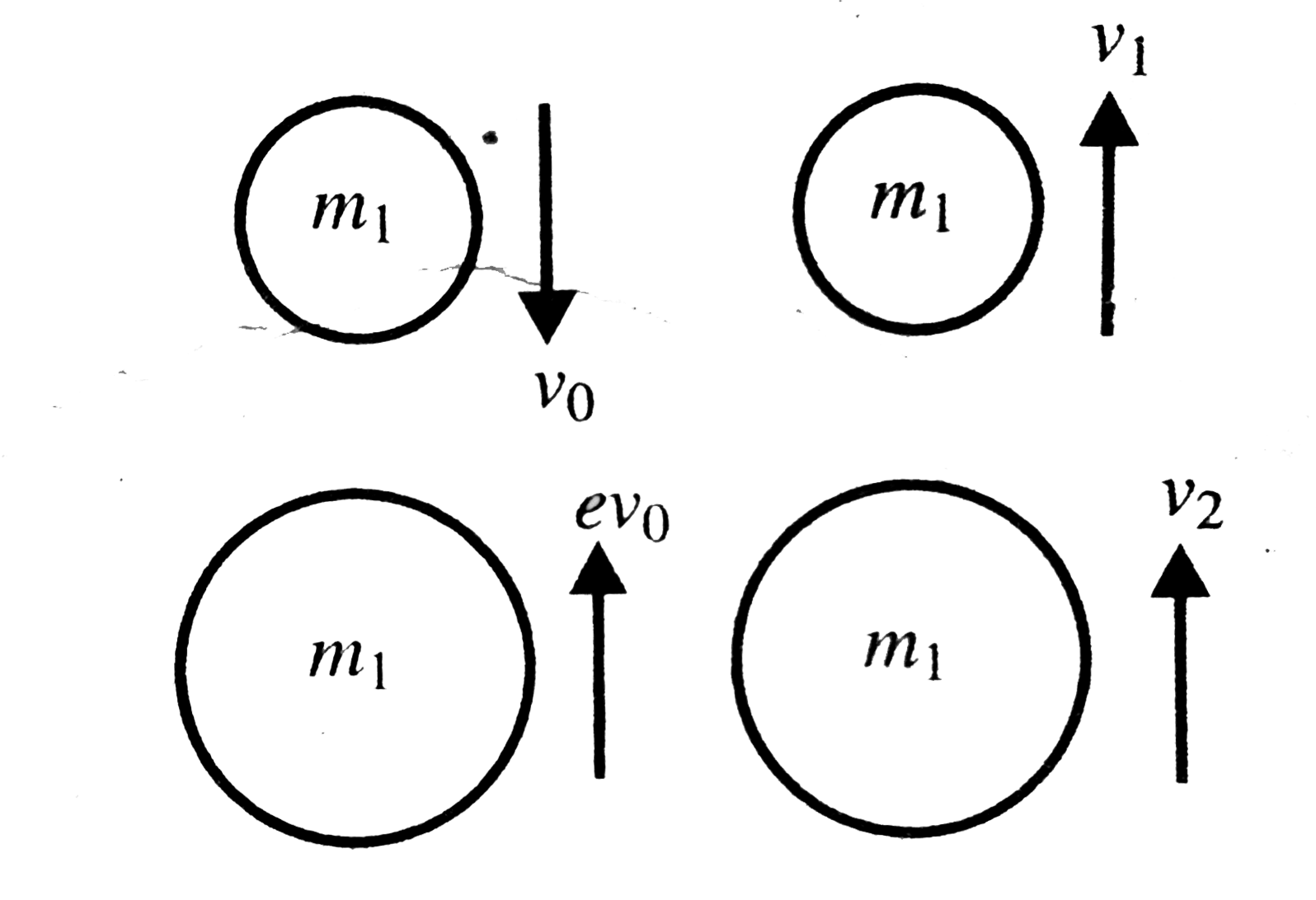
Newton's impact formula $- e [u_{1} - u_{2}] = v_{1} - v_{2}$
where $u_{1} = - v_{0}$ and $u_{2} = e v_{0}$
Then $- e [(- v_{0}) - (e v_{0})] = v_{1} - v_{2}$ .............ii
Solving eqn i and ii we have
$v_{1} = \frac{- (m_{1} - e m_{2})}{m_{1} + m_{2}} v_{0} + \frac{(1 + e) m_{2}}{m_{1} + m_{2}} e v_{0}$
Putting $m_{1} = m_{2}, e = \frac{1}{2}$ and $v_{0} = \sqrt{2 g h}$ we have $v_{1} = \sqrt{\frac{g h}{32}} ↑ ⏐ ⏐ ⏐ ⏐ ⏐$

Updated on:21/07/2023