Two strips of metal are riveted together at their ends by four rivets, each of diameter 6 mm. Assume that each rivet is to carry one quarter of the load. If the shearing stress on the rivet is not to exceed 6.9×107Pa, the maximum tension that can be exerted by the riveted strip is
To find the maximum tension that can be exerted by the riveted strip, we can follow these steps:
Step 1: Determine the area of one rivet
The area A of a rivet can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the rivet.
Given the diameter of each rivet is 6 mm, the radius r is:
r=6 mm2=3 mm=3×10−3 m
Now, substituting the radius into the area formula:
A=π(3×10−3)2=π(9×10−6) m2=9π×10−6 m2
Step 2: Calculate the maximum shear force for one rivet
The maximum shear force F that one rivet can carry is given by the product of the shear stress τ and the area A:
F=τ⋅A
Given that the maximum shearing stress τ is 6.9×107 Pa:
F=6.9×107 Pa×9π×10−6 m2
Step 3: Calculate the total maximum shear force for all rivets
Since there are 4 rivets, the total maximum shear force Ftotal is:
Ftotal=4×F
Substituting the expression for F:
Ftotal=4×(6.9×107 Pa×9π×10−6 m2)
Step 4: Calculate the maximum tension
The maximum tension T that can be exerted by the riveted strip is equal to the total maximum shear force:
T=Ftotal
Calculating this gives:
T=4×(6.9×107×9π×10−6)
Calculating 9π≈28.26:
T=4×(6.9×107×28.26×10−6)
T=4×(1.95×103)≈7.8×103 N
Conclusion
The maximum tension that can be exerted by the riveted strip is:
7.8×103 N
The area A of a rivet can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the rivet.
r=6 mm2=3 mm=3×10−3 m
A=π(3×10−3)2=π(9×10−6) m2=9π×10−6 m2
The maximum shear force F that one rivet can carry is given by the product of the shear stress τ and the area A:
F=τ⋅A
Given that the maximum shearing stress τ is 6.9×107 Pa:
F=6.9×107 Pa×9π×10−6 m2
Since there are 4 rivets, the total maximum shear force Ftotal is:
Ftotal=4×F
Substituting the expression for F:
Ftotal=4×(6.9×107 Pa×9π×10−6 m2)
The maximum tension T that can be exerted by the riveted strip is equal to the total maximum shear force:
T=Ftotal
Calculating this gives:
T=4×(6.9×107×9π×10−6)
Calculating 9π≈28.26:
T=4×(6.9×107×28.26×10−6)
T=4×(1.95×103)≈7.8×103 N
The maximum tension that can be exerted by the riveted strip is:
7.8×103 N
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - EXERCISE
21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE
31 Videos
- MOTION IN A PLANE BOOK - NCERT ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - EXERCISE
32 Videos
Similar Questions
Two long metallic strips are joined together by two rivets each of radius 2mm. Each rivet can withstand a maximum shearing stress of 1.5×109N/m2. Assuming that each rivet shares the stretching load equally, the maximum tensile force the strip can exert without rupture is
View SolutionTwo long metallic strips are joined together by two rivets each of radius 2mm. Each rivet can withstand a maximum shearing stress of 1.5×109N/m2. Assuming that each rivet shares the stretching load equally, the maximum tensile force the strip can exert without rupture is
View Solution
Knowledge Check
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6mm. What is the maximum tension that can be exterted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9×107Pa? Assume that each rivet is to carry one quarter of the load .
A2×103NB3.9×103NC7.8×103ND15.6×103NThe chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
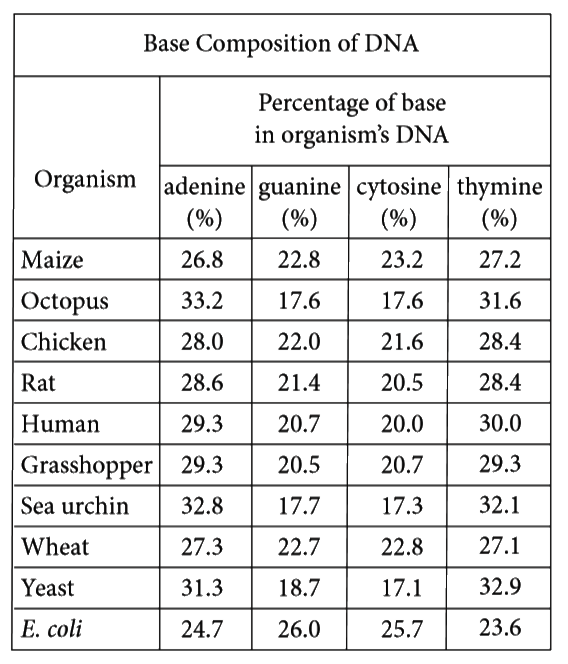
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
31. Based on the table, is the percentage of adenine in each organism’s DNA the same or does it vary, and which statement made by the authors is most consistent with that data?AThe same, “Two of . . . pyrimidines” (lines 6-8)BThe same, “The important . . . structure” (lines 25-26)CIt varies, “Adenine . . . thymine” (lines 36-38)DIt varies, “It follows . . . information” (lines 41-45)The chemical formula of deoxyribonucleic acid
(DNA) is now well established. The molecule is a
very long chain, the backbone of which consists of a
regular alternation of sugar and phosphate groups.
5 To each sugar is attached a nitrogenous base, which
can be of four different types. Two of the possible
bases—adenine and guanine—are purines, and the
other two—thymine and cytosine—are pyrimidines.
So far as is known, the sequence of bases along the
10 chain is irregular. The monomer unit, consisting of
phosphate, sugar and base, is known as a nucleotide.
The first feature of our structure which is of
biological interest is that it consists not of one chain,
but of two. These two chains are both coiled around
15 a common fiber axis. It has often been assumed that
since there was only one chain in the chemical
formula there would only be one in the structural
unit. However, the density, taken with the X-ray
evidence, suggests very strongly that there are two.
20. The other biologically important feature is the
manner in which the two chains are held together.
This is done by hydrogen bonds between the bases.
The bases are joined together in pairs, a single base
from one chain being hydrogen-bonded to a single
25 base from the other. The important point is that only
certain pairs of bases will fit into the structure.
One member of a pair must be a purine and the other
a pyrimidine in order to bridge between the two
chains. If a pair consisted of two purines, for
30 example, there would not be room for it.
We believe that the bases will be present almost
entirely in their most probable forms. If this is true,
the conditions for forming hydrogen bonds are more
restrictive, and the only pairs of bases possible are:
35 adenine with thymine, and guanine with cytosine.
Adenine, for example, can occur on either chain, but
when it does, its partner on the other chain must
always be thymine.
The phosphate-sugar backbone of our model is
40 completely regular, but any sequence of the pairs of
bases can fit into the structure. It follows that in a
long molecule many different permutations are
possible, and it therefore seems likely that the precise
sequence of bases is the code which carries the
45 genetical information. If the actual order of the bases
on one of the pair of chains were given, one could
write down the exact order of the bases on the other
one, because of the specific pairing. Thus one chain
is, as it were, the complement of the other, and it is
50 this feature which suggests how the deoxyribonucleic
acid molecule might duplicate itself.
The table shows, for various organisms, the percentage of
each of the four types of nitrogenous bases in that
organism’s DNA.
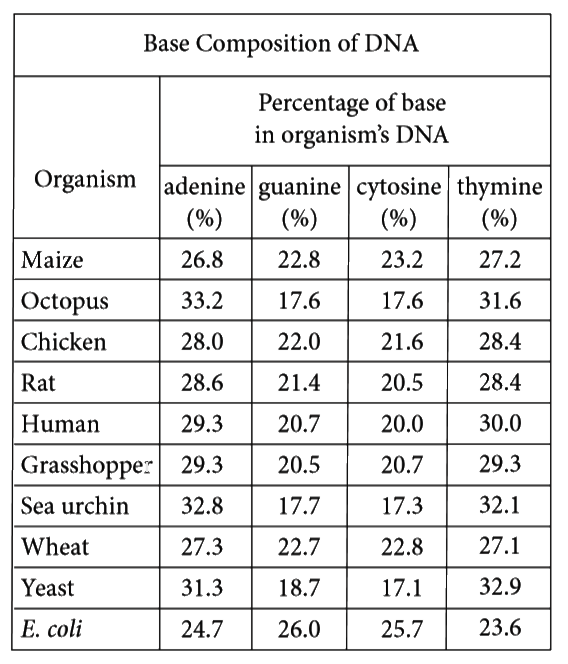
Adapted from Manju Bansal, “DNA Structure: Revisiting the
Watson-Crick Double Helix.” ©2003 by Current Science Association,
Bangalore
23. A student claims that nitrogenous bases pair randomly with one another. Which of the following statements in the passage contradicts the student’s claim?ALines 5-6 (“To each . . . types”)BLines 9-10 (“So far . . . irregular”)CLines 23-25 (“The bases . . . other”)DLines 27-29 (“One member . . . chains”)
Two spherical soap bubbles of diameters 10 cm and 6 cm are formed, one at each end of a narrow horizontal glass tube. If the surface tension of the soap solution is 0.03Nm−1, then the pressure difference in pascal between the two ends of the tube is
View SolutionA mass of 20kg is attached to one end of a steel wire 50cm long and is rotated in a horizontal circle. The area of cross-section of the wrie is 10−6m2 and the breaking stress for it is 4.8×107Pa. Calculate the maximum velocity with which the mass can be rotated.
View SolutionTwo narrow bores of diameters 3.0mm and 6.0 mm are joined together to form a U-shaped tube open at both ends. If th U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3×10−2Nm−1. Take the angle of contact to be zero. and density of water to be 1.0×103kg/m3.
(g=9.8ms−2)
View SolutionTwo narrow bores of diameters 3.0mm and 6.0 mm are joined together to form a U-shaped tube open at both ends. If th U-tube contains water, what is the difference in its levels in the two limbs of the tube? Surface tension of water at the temperature of the experiment is 7.3×10−2Nm−1. Take the angle of contact to be zero. and density of water to be 1.0×103kg/m3.
(g=9.8ms−2)
View SolutionTwo capillary tubes of diameters 3.0mm and 6.0mm are joined together to form a U-tube open at both ends. If the U-tube is filled with water, what is the difference in its levels in the two limbs of the tube ? Surface tension of water at the temperature of the experiment is 7.3×102N/m. Take the angie of contact to be zero and density of water to be 103kg/m3(g=9.8m/s2)
View Solution
