ABC and ADC are two right triangles with common hypotenuse AC. Prove that ∠CAD=∠CBD.
Proof: Since ∠ABC and ∠ADC are 90∘.
These angles are in the semi-circle
Thus, both the triangles are lying in the semi-circle and AC is the diameter of the circle.
Points A,B,C and D are concyclic.
Hence, CD is the chord.
∠CAD=∠CBD (Angles in the same segment of the circle)
Topper's Solved these Questions
Similar Questions
In Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
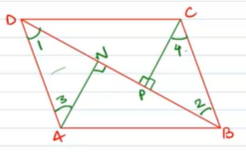 View Solution
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionIn right triangle ABC , right angle at C, M is the mid-point of the hypotenuse AB. C is jointed to M and produced to a point D such that DM=CM. Point D is joined to point B. Show that AMC≅BMD (ii) ∠DBC=90∘ (iii)DBC≅ACB (iv) CM=12AB
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionTriangles ABC and +DBC are on the same base BC with A, D on opposite side of line BC, such that ar(△ABC)=ar(△DBC). Show that BC bisects AD.
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View SolutionIn ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionABC is a triangle in which D is the mid-point of BC and E is the mid-point of AD. Prove that area of △BED=14areaof△ABC. GIVEN : A ABC,D is the mid-point of BC and E is the mid-point of the median AD. TO PROVE : ar(△BED)=14ar(△ABC).
View SolutionABC is a triangle. D is the mid point of BC. If AD is perpendicular to AC, then prove that cosA .cosC=2(c2−a2)3ac .
View Solution

