are respectively the smallest and longest sides of a quadrilateral
(see Fig. 7.50). Show that and

Given: AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD
To prove: ∠A > ∠C and ∠B > ∠D
Let's join vertex A to C as shown below.
In the above ΔABC,
AB < BC (given AB is the smallest side of quadrilateral ABCD)
∠ACB < ∠BAC (Angle opposite to the smaller side is smaller) ... (1)
In ΔADC,
AD < CD (given CD is the largest side of quadrilateral ABCD)
∠ACD < ∠CAD (Angle opposite to the smaller side is smaller) ... (2)
On adding Equations (1) and (2), we obtain
∠ACB + ∠ACD < ∠BAC + ∠CAD
∠C < ∠A
This means, ∠A > ∠C
Hence Proved.
Let's now join BD.
In ΔABD,
AB < AD (Given AB is the smallest side of quadrilateral ABCD)
∠ADB < ∠ABD (Angle opposite to the smaller side is smaller) ...(3)
In ΔBDC,
BC < CD (Given CD is the largest side of quadrilateral ABCD)
∠BDC < ∠CBD (Angle opposite to the smaller side is smaller) ... (4)
On adding equations (3) and (4), we obtain
∠ADB + ∠BDC < ∠ABD + ∠CBD
∠D < ∠B
This means, ∠B > ∠D
Hence, proved.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.18videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Solved Examples9videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.28videos
TRIANGLES
- BOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.93videos
SURFACE AREAS AND VOLUMES
Similar Questions
In Figure, AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D.
View SolutionIn Figure, AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD. Show that ∠A>∠C and ∠B>∠D
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn quadrilateral ABCD ,side DC is largest show that AB + AD > DC - BC
View SolutionIf the sides of a quadrilateral ABCD touch a circle prove that
AB+CD=BC+AD.View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
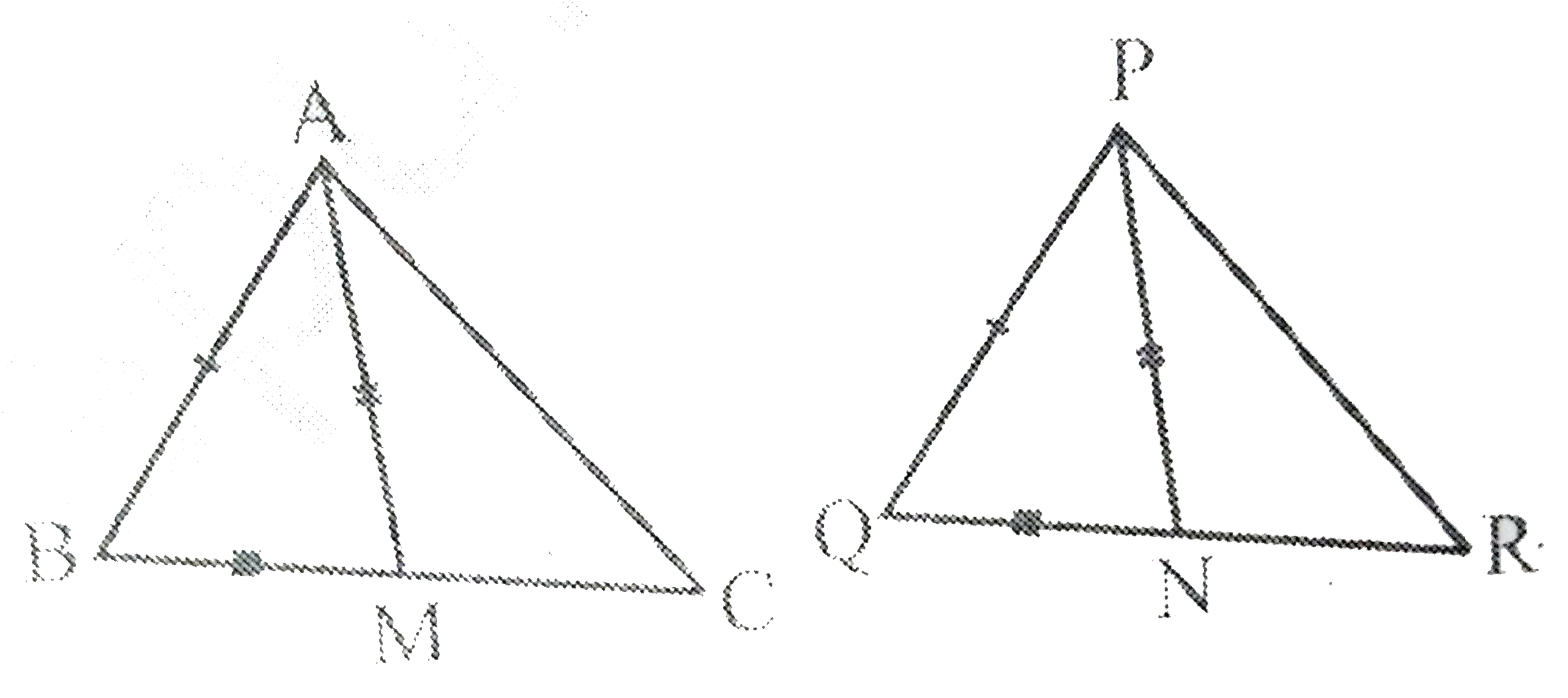
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
 View Solution
View SolutionP, Q, R and S are respectively the mid-points of sides AB, BC, CD and DA of quadrilateral ABCD in which AC=BD and AC⊥BD. Prove that PQRS is a square.
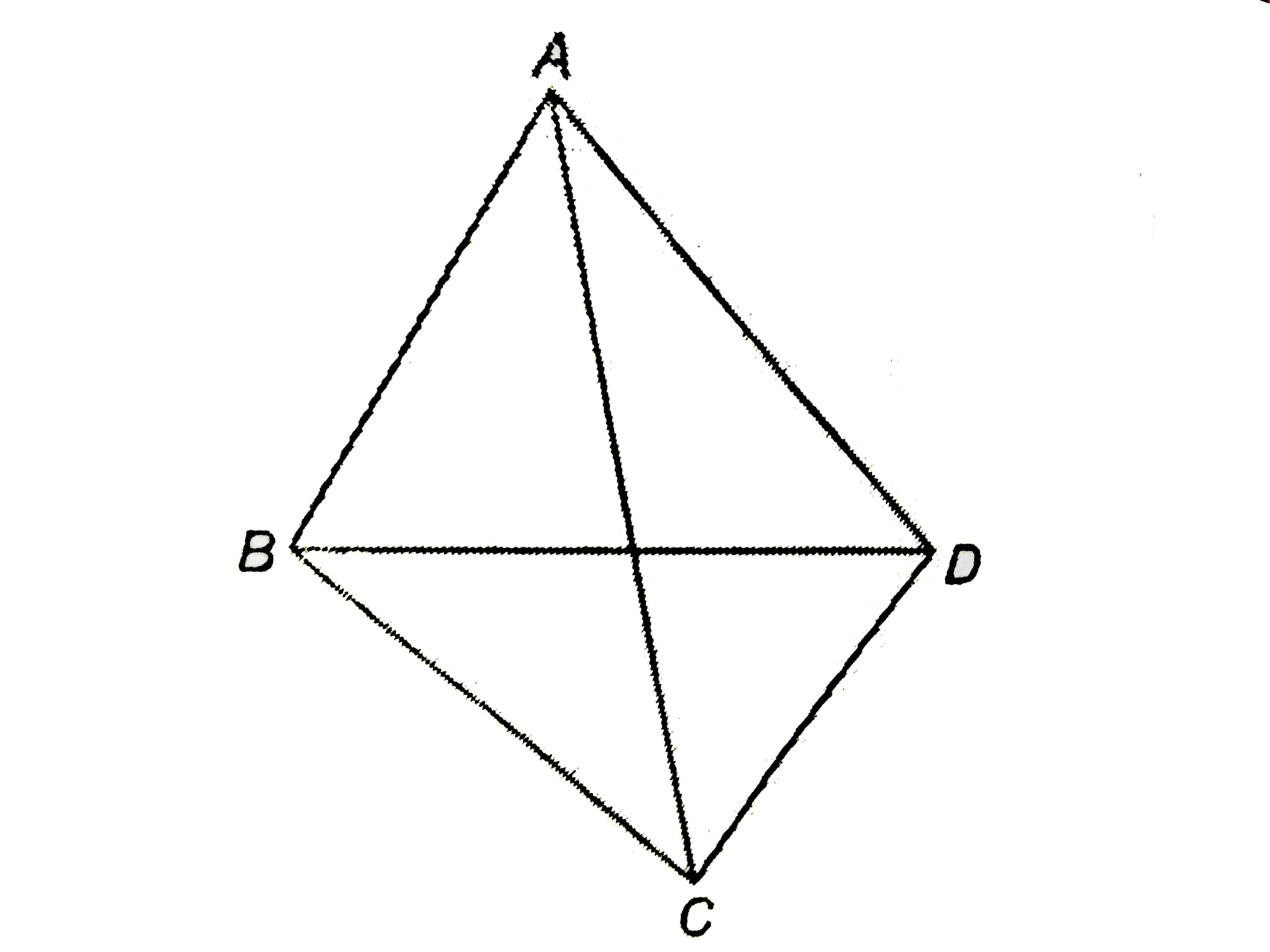
View SolutionThe given figure shows a quadrilateral ABCD. Prove that :
AB+BC+CD+DA>AC+BD
 View Solution
View Solution

