Doubtnut Promotions Sticky

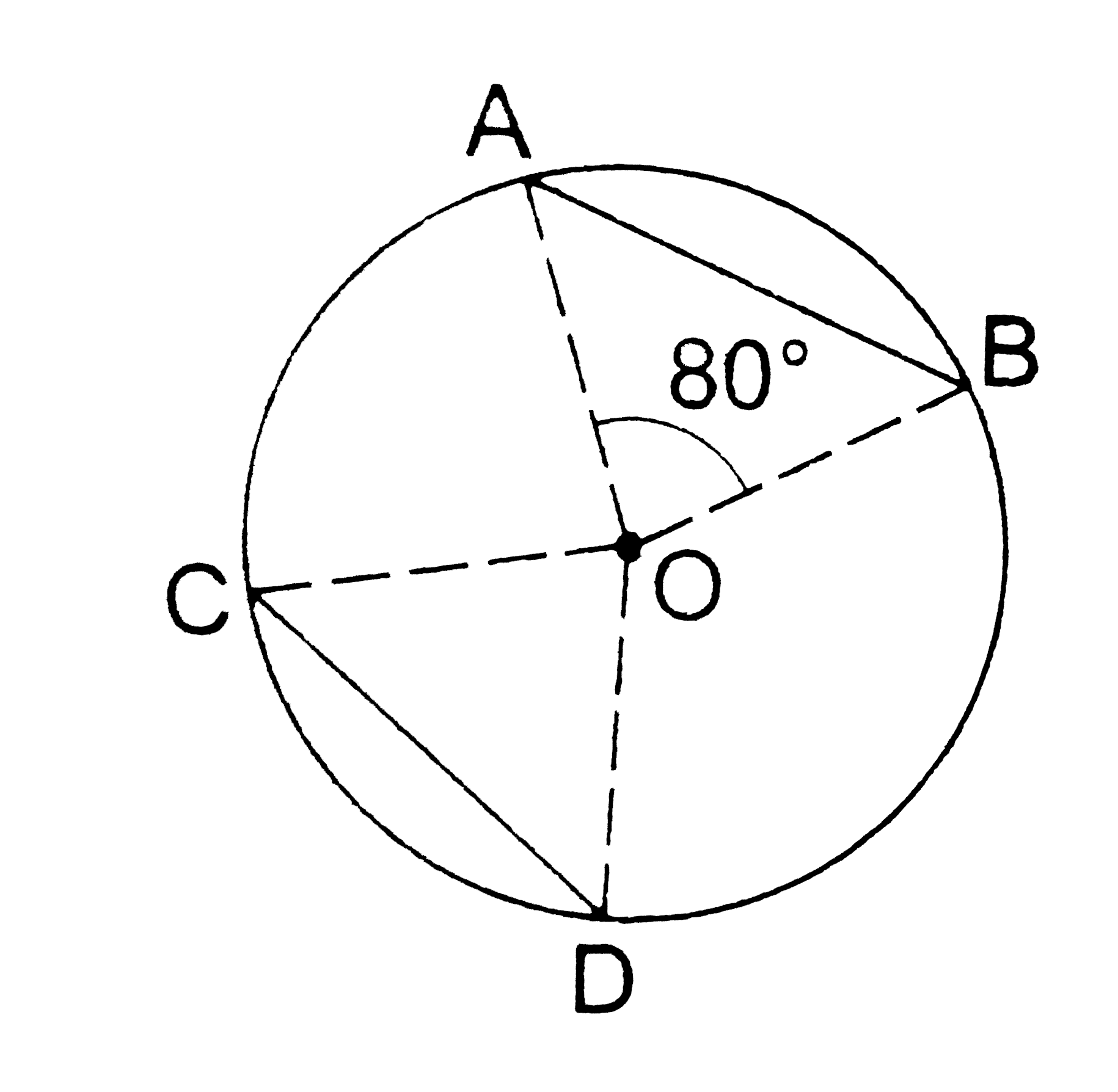
AB and CD are two equal to chord of a circle with centre O such that ∠AOB=80∘. Then ∠COD=?
AB and CD are two equal to chord of a circle with centre O such that / AOB = 80^(@). Then / COD = ?

A

100∘

B

80∘

C

120∘

D

40∘

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Since equal chords of a circle subtend equal angles at the centre , so ∠COD=∠AOB=80∘

|
Updated on:21/07/2023
Class 9MATHSCIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    AB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB =10cm , CD =24 cm and the distance between AB and CD is 17cm. Find the radius of the circle.

    A13 cm
    B14 cm
    C15 cm
    D16 cm
  • Question 2 - Select One

    In the given figureAB and CD are two parallel chords of a circle with centre O and radius 5 cm. Also, AB = 8 cm andCD = 6cm. If OP perpendicular to AB andOQ perpendicular to CD,then determine the length of PQ
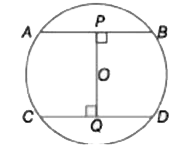    ocr_image

    A7 cm
    B10 cm
    C8 cm
    DNone of these
  • Question 3 - Select One

    Two chords AB and CD of a circle with centre O intersect at P. If ∠APC=40∘. Then the value of ∠AOC+∠BOD is

    A50∘
    B60∘
    C80∘
    D120∘