ABC is a isosceles right angled triangle, right angled at C. prove that AB2=2AC2
To prove that AB2=2AC2 in the isosceles right triangle ABC with the right angle at C:
1. Identify the Triangle:
We have triangle ABC which is isosceles and right-angled at C. This means that AC=BC.
2. Label the Sides:
Let AC=BC=x. Since AC and BC are the legs of the triangle, we can denote their lengths as x.
3. Apply the Pythagorean Theorem:
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse AB is equal to the sum of the squares of the other two sides:
AB2=AC2+BC2
4. Substitute the Values:
Since AC=x and BC=x, we can substitute these values into the equation:
AB2=x2+x2
5. Simplify the Equation:
Combine the terms on the right side:
AB2=2x2
6. Relate to AC:
Since AC=x, we can rewrite x2 as AC2:
AB2=2AC2
7. Conclusion:
We have proved that AB2=2AC2.
We have triangle ABC which is isosceles and right-angled at C. This means that AC=BC.
Let AC=BC=x. Since AC and BC are the legs of the triangle, we can denote their lengths as x.
According to the Pythagorean theorem, in a right-angled triangle, the square of the hypotenuse AB is equal to the sum of the squares of the other two sides:
AB2=AC2+BC2
Since AC=x and BC=x, we can substitute these values into the equation:
AB2=x2+x2
Combine the terms on the right side:
AB2=2x2
Since AC=x, we can rewrite x2 as AC2:
AB2=2AC2
We have proved that AB2=2AC2.
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Very Short Questions
9 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Revision Exercise Short Questions
10 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLES EXERCISE - Exercise 6c
11 Videos
- STATISTICS BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
5 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHANCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
Knowledge Check
A statements of Assertion (A) is followed by a statement of Reason (R ). Mark the correct choice as.
Assertion (A): ABC is an isoseles triangle right triangle , right angled at C. Then AB2=3AC2.
Reason (R ): In an isosceles triangle ABC if AC = BC and AB2=2AC2 then ∠C=90∘.ABoth A and R are true R is the correct explanation for A.BBoth A and R are true nad R is not correct explanation for A.CA is true but R is false.DA is false but R is true.ABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
A30 unitB20 unitC40 unitDNone of these
ABC is an isosceles triangle right-angled at C. Prove that AB2=2AC2.
View SolutionIn figure ABC is an isosceles triangle , right angled at C . Therefore
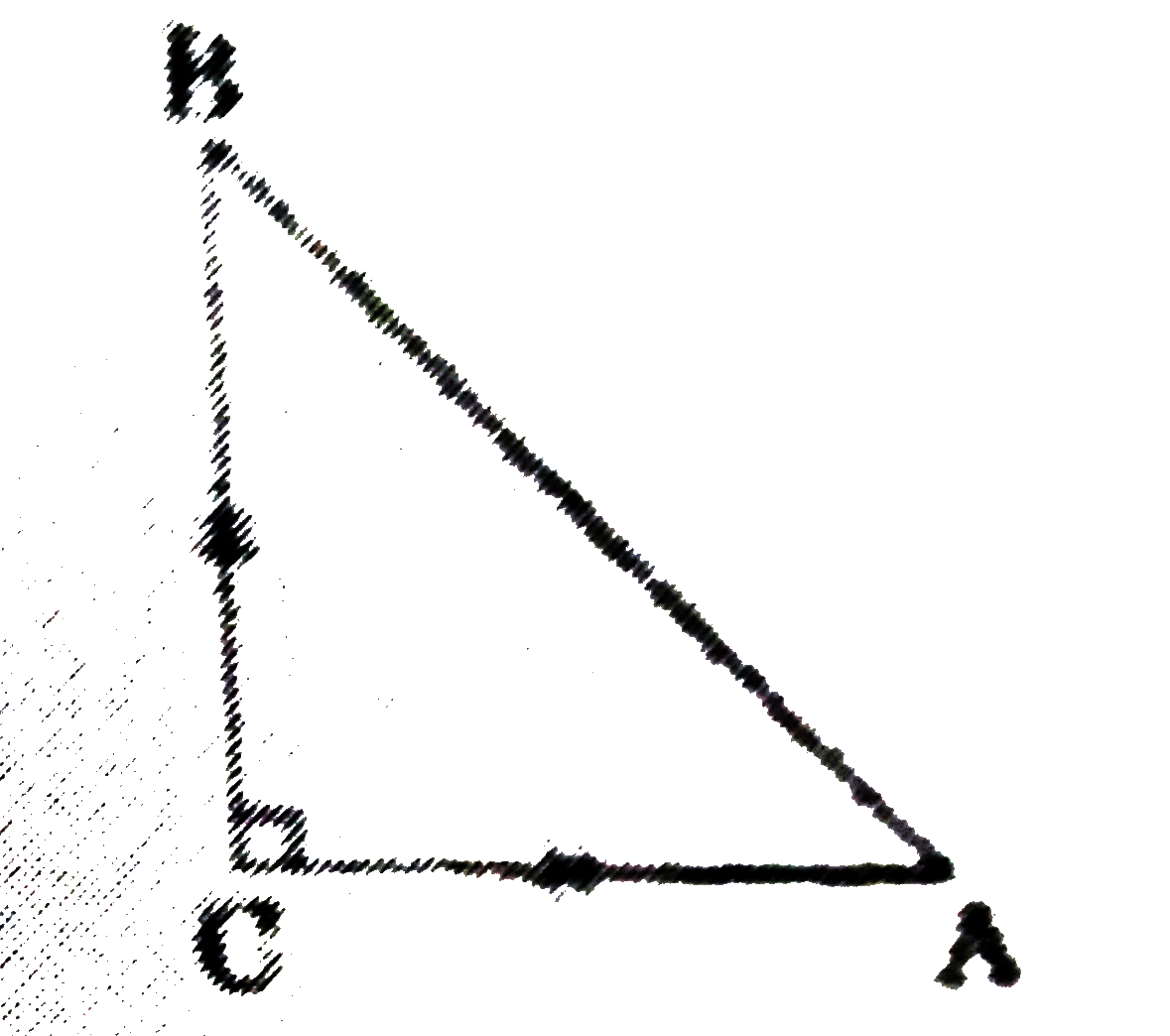
View SolutionIn right angled triangle ABC, right angled at C, show that tanA+tanB=c2ab.
View SolutionABC is an isosceles right-triangle right angled at C such that AC=5 cm. Then, AB= 2.5 cm (b) 5√2 cm 10 cm (d) 5 cm
View SolutionABC is a right triangle right-angled at CandAC=√3BC . Prove that ∠ABC=600.
View SolutionConsider an isoceles right angled triangle ΔABC at C, then AB2= ....times AC2.
View Solution
