ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC=140∘, than ∠BAC is equal to
80∘
50∘
40∘
30∘
The correct Answer is:B
To solve the problem step by step, we will use properties of cyclic quadrilaterals and the fact that angles subtended by a diameter are right angles.
1. Identify the Given Information:
- ABCD is a cyclic quadrilateral.
- AB is the diameter of the circle.
- Angle ADC = 140°.
2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the sum of the opposite angles is 180°.
- Therefore, we can write:
Angle ADC+Angle ABC=180°
- Substituting the known value:
140°+Angle ABC=180°
3. Solve for Angle ABC:
- Rearranging the equation gives:
Angle ABC=180°−140°=40°
4. Use the Diameter Property:
- Since AB is the diameter, angle ACB is a right angle (90°) because an angle subtended by a diameter at the circumference is always 90°.
5. Use the Triangle Angle Sum Property:
- In triangle ACB, the sum of the angles is 180°:
Angle BAC+Angle ACB+Angle ABC=180°
- Substituting the known angles:
Angle BAC+90°+40°=180°
6. Solve for Angle BAC:
- Rearranging the equation gives:
Angle BAC+130°=180°
- Therefore:
Angle BAC=180°−130°=50°
Final Answer:
Angle BAC = 50°.
---
- ABCD is a cyclic quadrilateral.
- AB is the diameter of the circle.
- Angle ADC = 140°.
- In a cyclic quadrilateral, the sum of the opposite angles is 180°.
- Therefore, we can write:
Angle ADC+Angle ABC=180°
- Substituting the known value:
140°+Angle ABC=180°
- Rearranging the equation gives:
Angle ABC=180°−140°=40°
- Since AB is the diameter, angle ACB is a right angle (90°) because an angle subtended by a diameter at the circumference is always 90°.
- In triangle ACB, the sum of the angles is 180°:
Angle BAC+Angle ACB+Angle ABC=180°
- Substituting the known angles:
Angle BAC+90°+40°=180°
- Rearranging the equation gives:
Angle BAC+130°=180°
- Therefore:
Angle BAC=180°−130°=50°
Angle BAC = 50°.
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.3
20 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
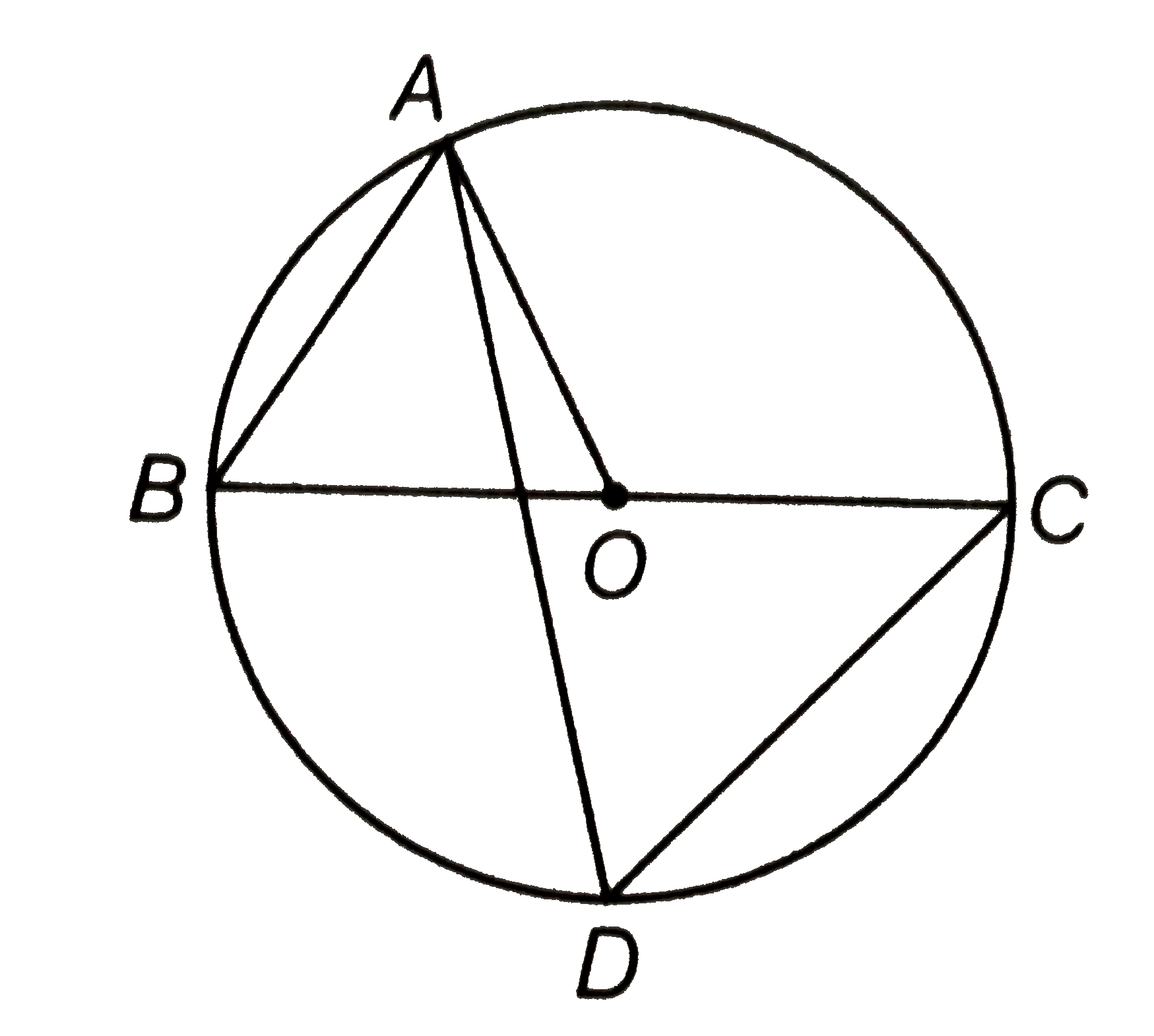
In the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.

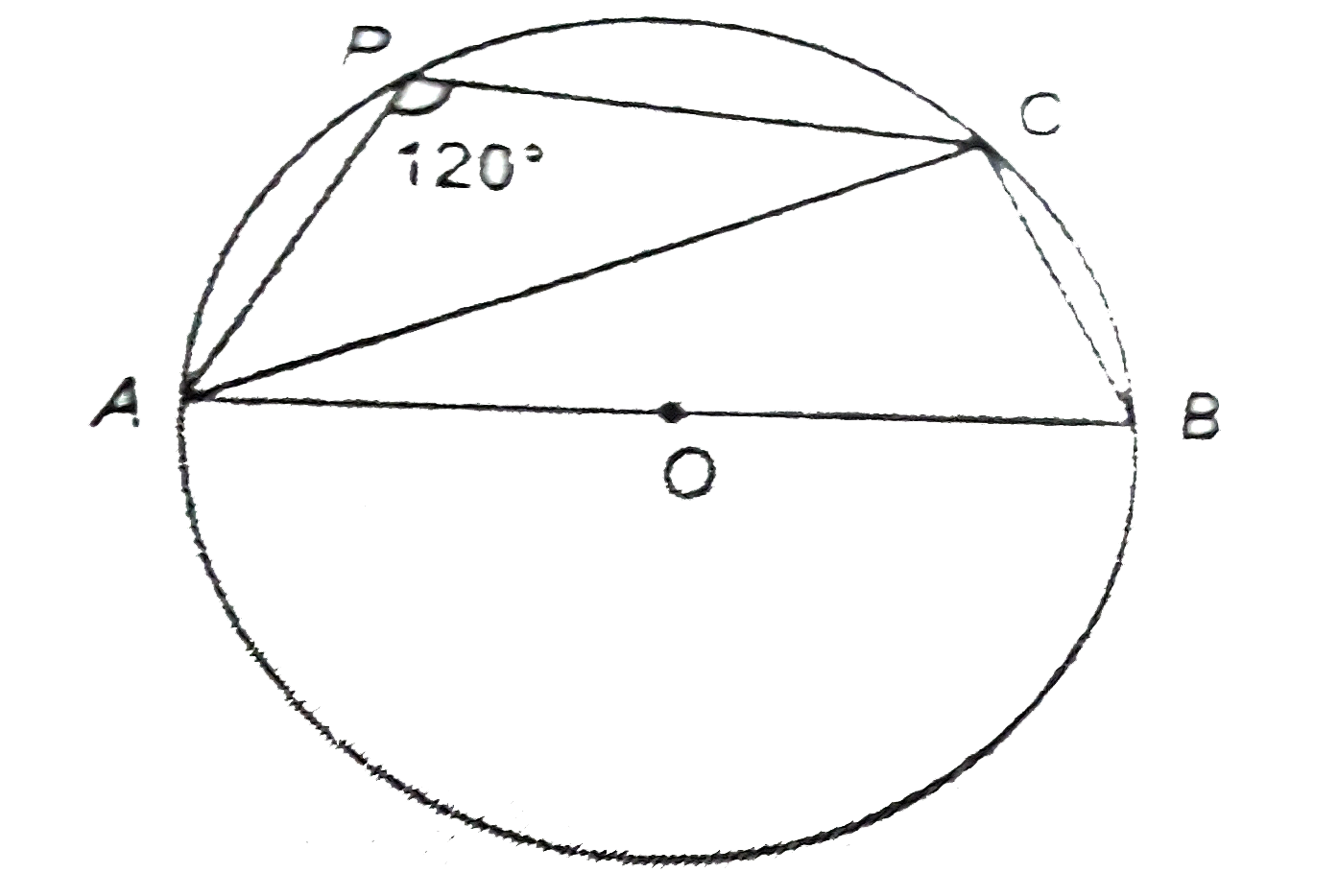
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
View SolutionIn figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Given ∠BED=65∘ , Calculate
(i) ∠DAB
(ii) ∠BDC
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
View SolutionABCD is a quadrilateral. Is AB+BC+CD+DA>AC+BD?
View SolutionIf the sides of a cyclic quadrilateral are 3,3,4,4, show that a circle be inscribed in it.
View SolutionIf ABCD is a cyclic quadrilateral such that 12tanA−5=0 and 5cosB+3=0 then tanC+tanD is equal to :
View SolutionIf ABCD is a cyclic quadrilateral such that 12tanA−5=0 and 5cosB+3=0 then tanC+tanD is equal to :
View Solution
