ABCD is a parallelogram and O is a point in its interior. Prove that
(i) ar(△AOB)+ar(△COD)
=12ar(||gm ABCD).
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
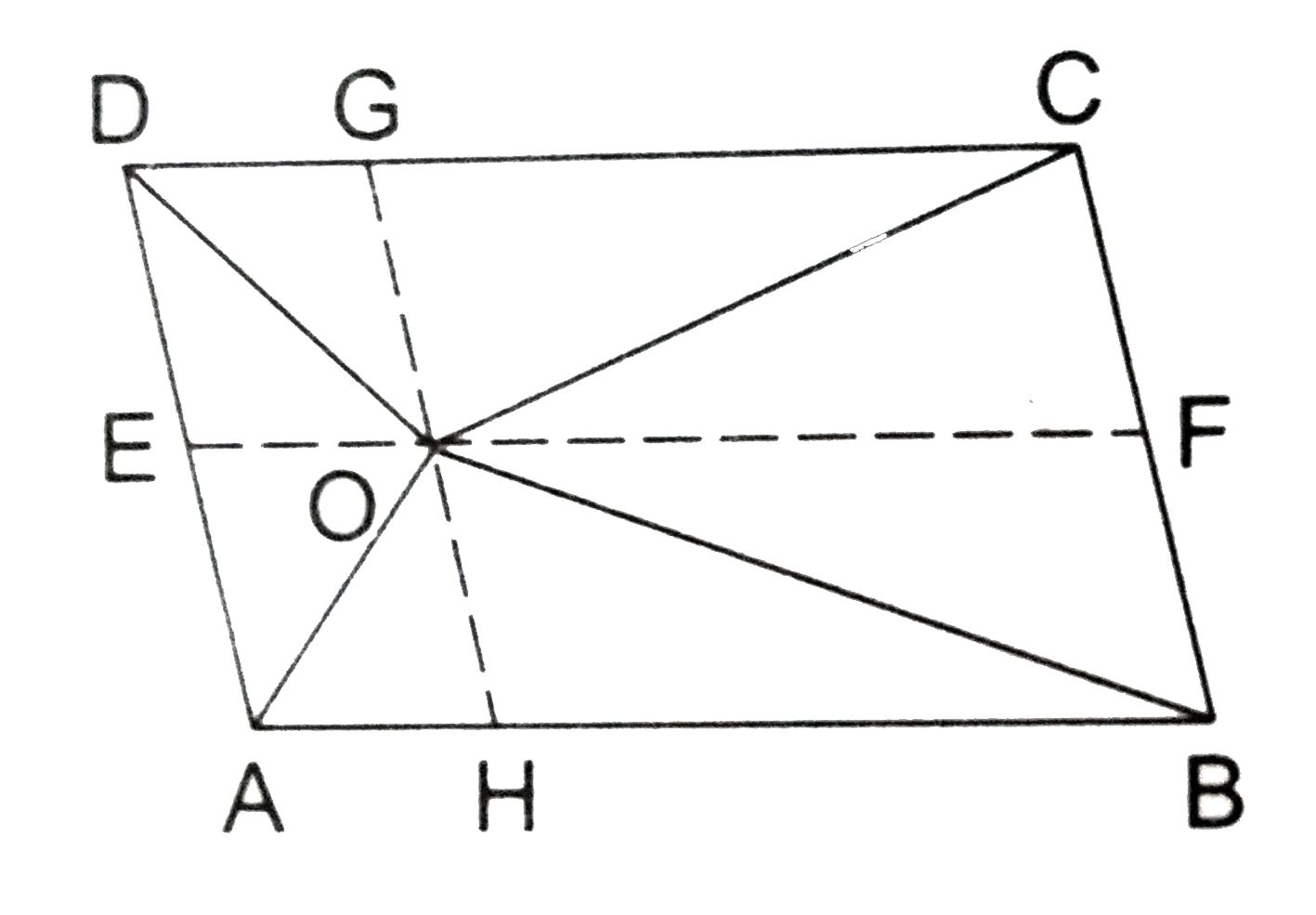
GIVEN A||gm ABCD and O is a point in its interior.
TO PROVE (i) ar(△AOB)+ar(△COD)=12ar(||gm ABCD),
(ii) ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC).
CONSTRUCTION Draw EOF||AB||DC and GOH||AD||BC.
PROOF △AOB and ||gm EABF being on the same base AB and between the same parallels AB and EF, we have
ar(△AOB)=12ar(||gm EABF). ...(i)
Similarly, ar(△COD)=12ar(||gm EFCD), ...(ii)
ar(△AOD)=12ar(||gm AHGD) ...(iii)
and ar(△BOC)=12ar(||gm BCGH) ...(iv)
Adding (i) and (ii), we get
ar(△AOB)+ar(△COD)=12ar(||gm EABF)+12ar(||gm EFCD)
=12ar(||gm ABCD). ...(v)
Adding (iii) and (iv), we get
aar(△AOD)+ar(△BOC)=12ar(||gm AHGD)+12ar(||gm BCGH)
=12ar(||gm ABCD). ...(vi)
∴ar(△AOB)+ar(△COD)=ar(△AOD)+ar(△BOC)
[from (v) and (vi)].
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
In the figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) ar(△APB)+ar(△PCD=12ar(ABCD)
(ii) ar(△APD)+ar(△PBC)=ar(△APB)+ar(△PCD)

View SolutionABCD is a parallelogram. X and Y are mid-points of BC and CD. Prove that ar(△AXY)=38ar(∣∣gmABCD)
View SolutionIn the adjoining figure, ABCD is a parallelogram and P is any points on BC. Prove that
ar(△ABP)+ar(△DPC)=ar(△PDA).
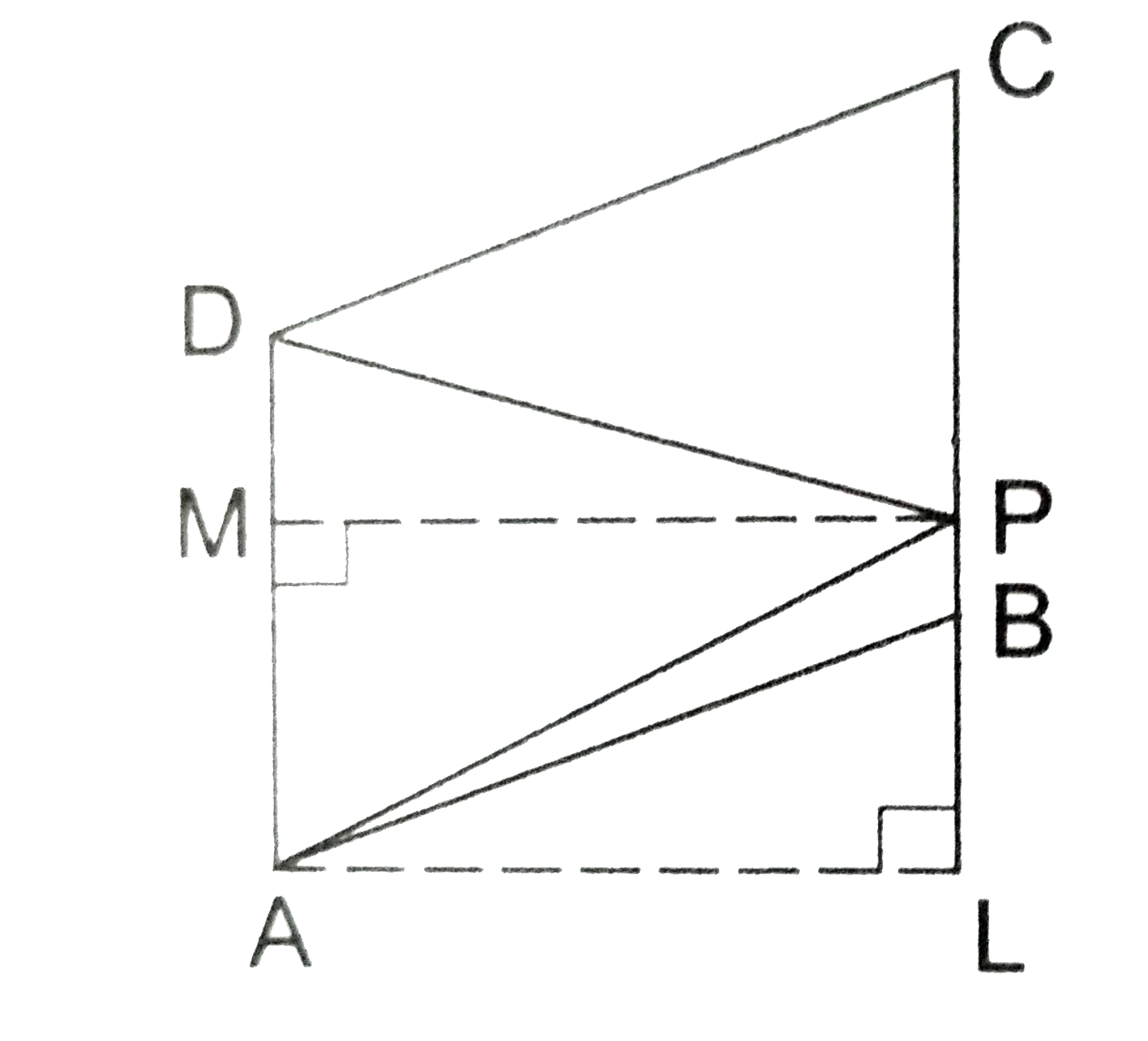
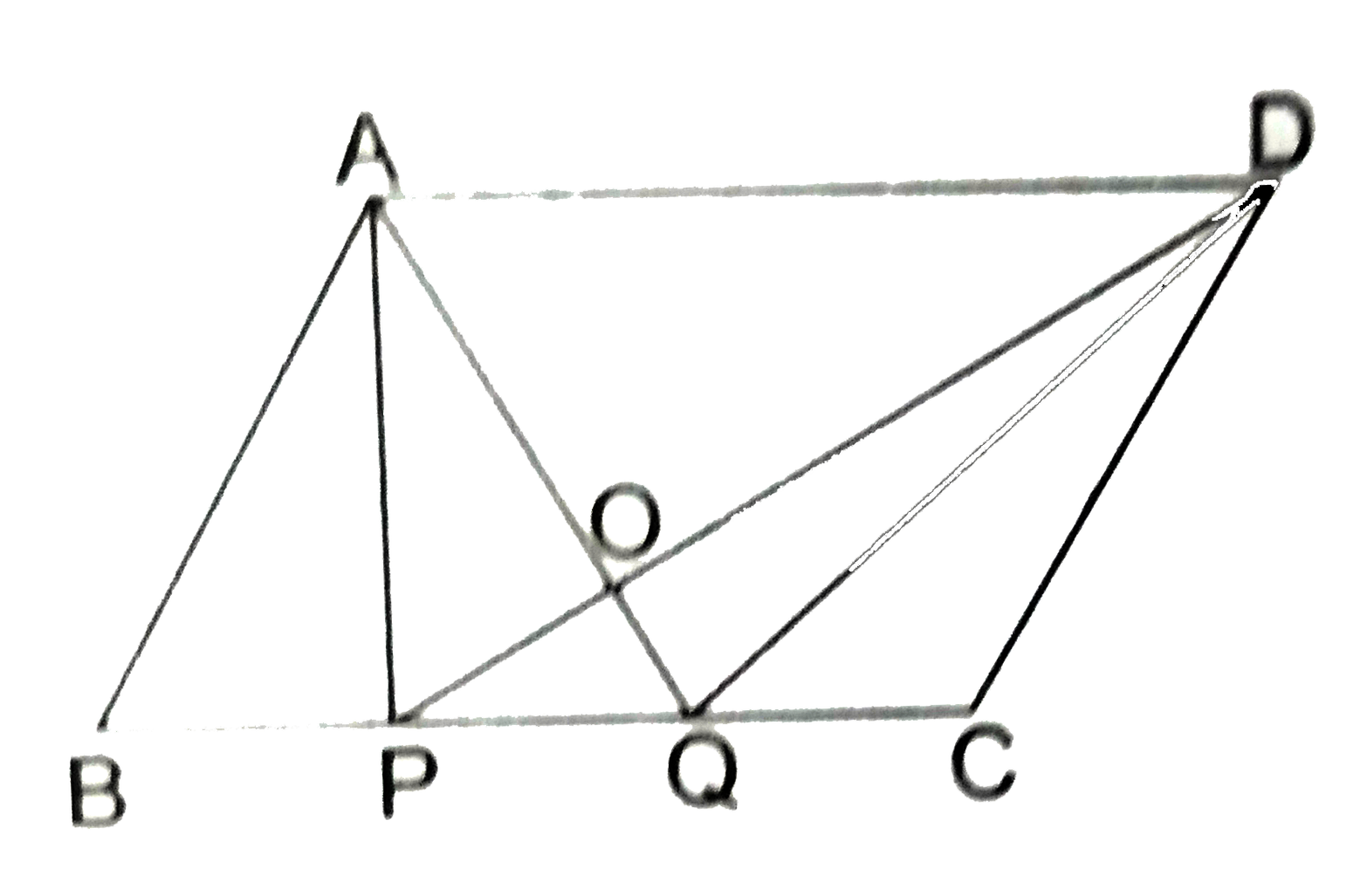
View SolutionIn the adjoining figure, ABCD is a parallelogram. Points P and Q on BC trisect BC. Prove that
ar(△APQ)=ar(△DPQ)=16ar(△ABCD).
View SolutionP is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△APD) = ar(△CPD).
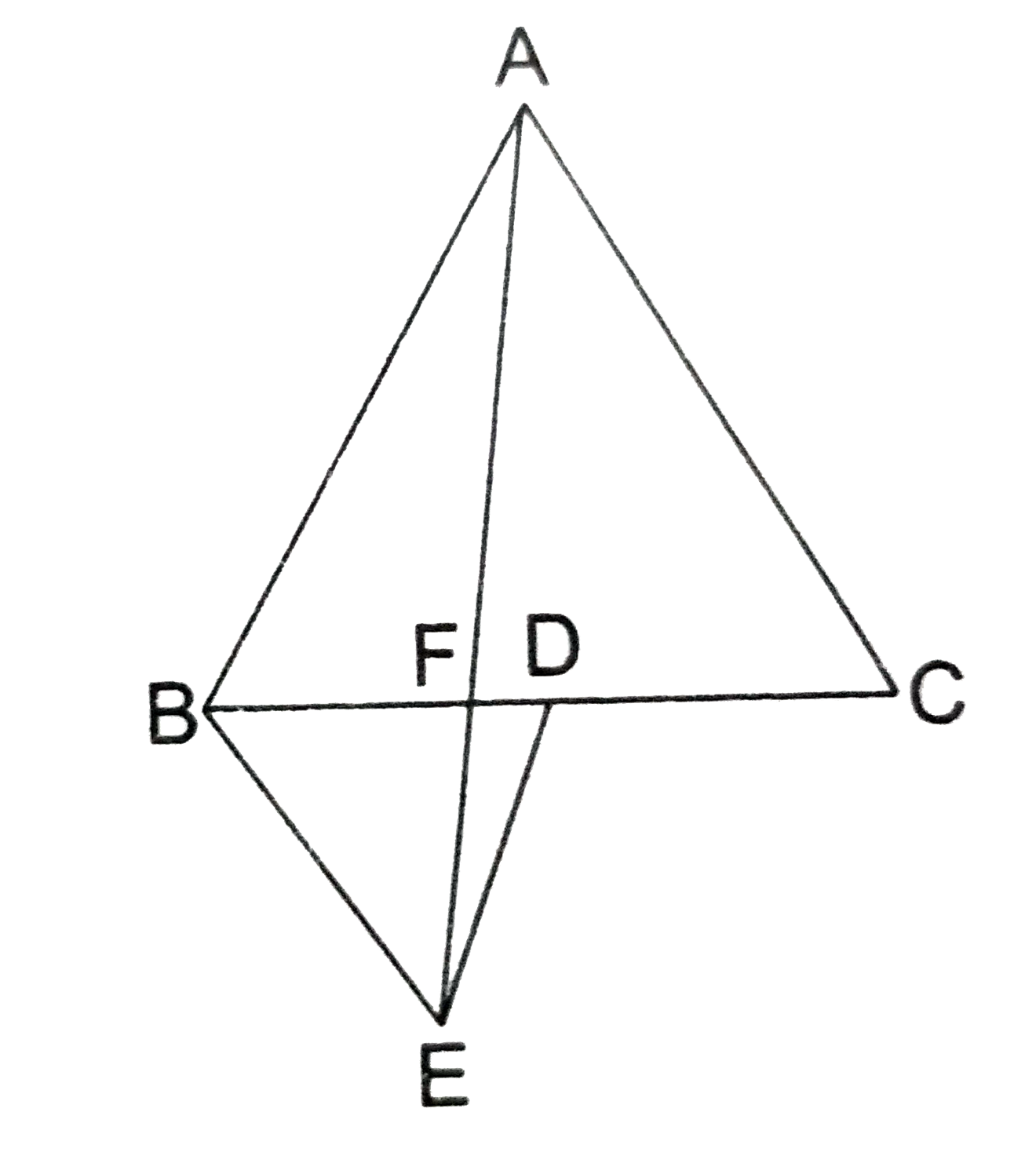
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).
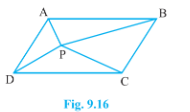
View SolutionIn Fig. 9.16, P is a point in the interior of a parallelogram ABCD. Show that(i) ar(APB)+ar(PCD)=12ar(ABCD)(ii) ar(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionABCD is a parallelogram and O is the point of intersection of its diagonals. If ar(△AOD)=4cm2 find ar(△AOB)
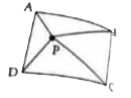
View SolutionIn the adjacent figure P is a point inside the parallelogram ABCD. Prove that
ar (APB) + ar (PCD) = 12 ar (ABCD)
View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
View Solution
