Bisectors of interior ∠ B and exterior ∠ ACD of a ΔABC intersect at the point T. prove that ∠BTC=12∠ BAC.
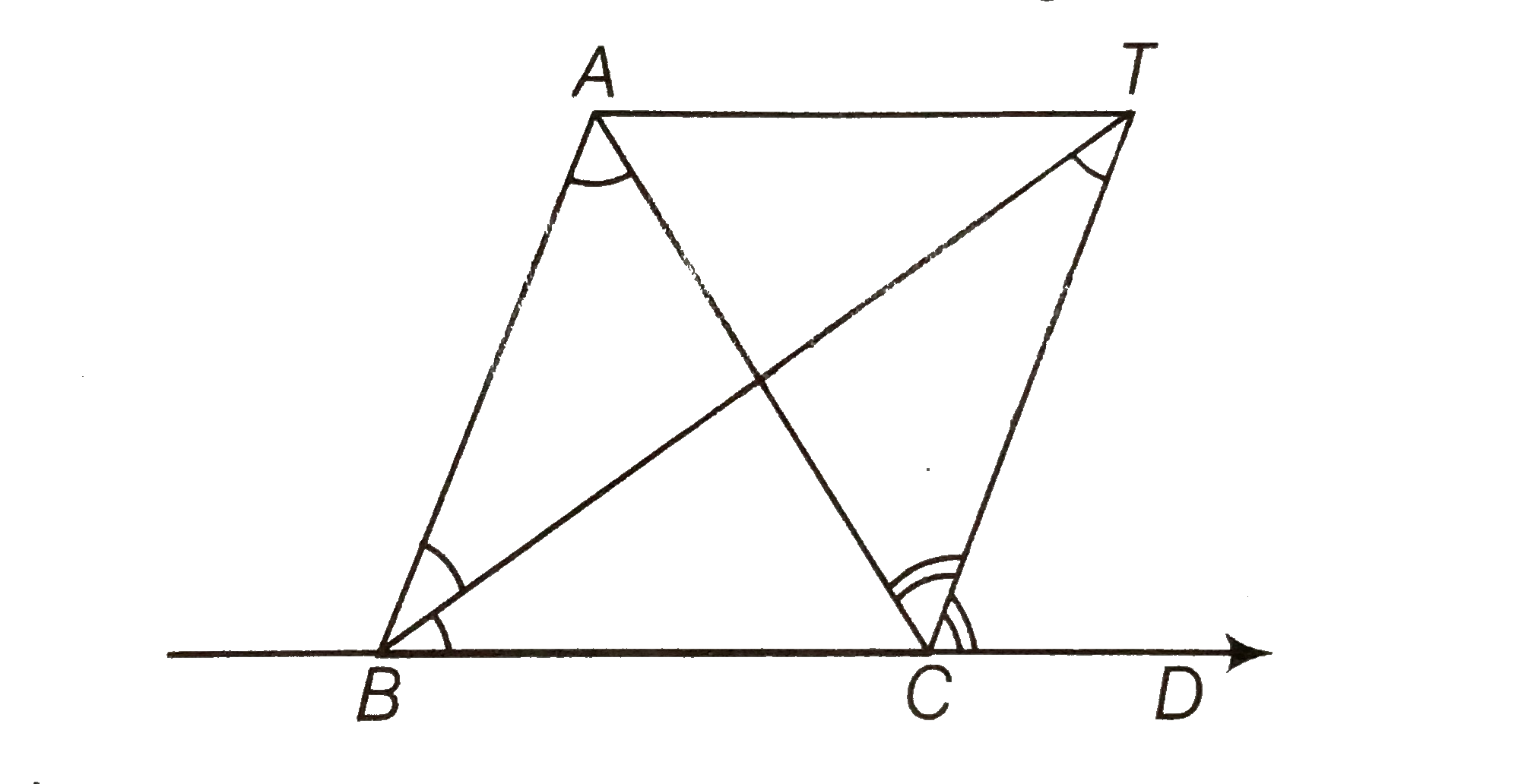
Given In Δ ABC, produce BC to DC and the bisectors of ∠ABC and ∠ACD meet at point T.
To prove ∠BTC = 1/2 ∠BAC
Proof In ΔABC, ∠C is an exterior angle.
∴ ∠ACD=∠ABC+∠CAB[exterior angle of a triangle is equal to the sum of two opposite angles]
⇒ 12∠ACD=12∠CAB+12∠ABC [dividing both sides by 2]
⇒ ∠TCD=12∠CAB+12∠ABC ....(i)
[∴CTisabisec→rof∠ACD⇒12∠ACD=∠TCD ]
In ΔBTC, ∠TCD=∠BTC+C∠CBT [exterior angles of a equal to the sum of two opposite interior angles]
⇒ ∠TCD=∠BTC+12∠ABC ....(ii) [∴BTbisectsof∠ABC⇒∠CBT=12∠ABC]
From Eqs. (i) and (ii) ,
1/2∠CAB+12∠ABC=∠BTC+12∠ABC
⇒ ∠BTC=12∠CAB
or ∠BTC=12∠ABC
Topper's Solved these Questions
Similar Questions
In ΔABC,AB=AC and the bisectors of angles B and C intersect at point O. Prove that
BO=OC
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionIn triangle LMN, bisector of interior angles at L and N intersect each other at point A. Prove that :
AM bisects angle LMN.
View SolutionBisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D,E and F respectively. Prove that angle EDF=90∘−12∠A
View SolutionThe bisector of interior ∠A of ABC meets BC in D, and the bisector of exterior ∠A meets BC produced in E. Prove that BDBE=CDCE.
View SolutionConstruct a triangle ABC which angle ABC=75∘,AB=5 cmandBC=6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisector intersect each other at point P, prove that P is equidistant from B and C, and also from AC and BC.
View SolutionThe bisectors of angles A and B of a scalene triangle ABC meet at O.
What is the point O called ?
View SolutionIn ΔABC, AB = AC and the bisectors of angles B and C intersect at point O. Prove that :
(i) BO = CO
(ii) AO bisects angle BAC.
View Solution
