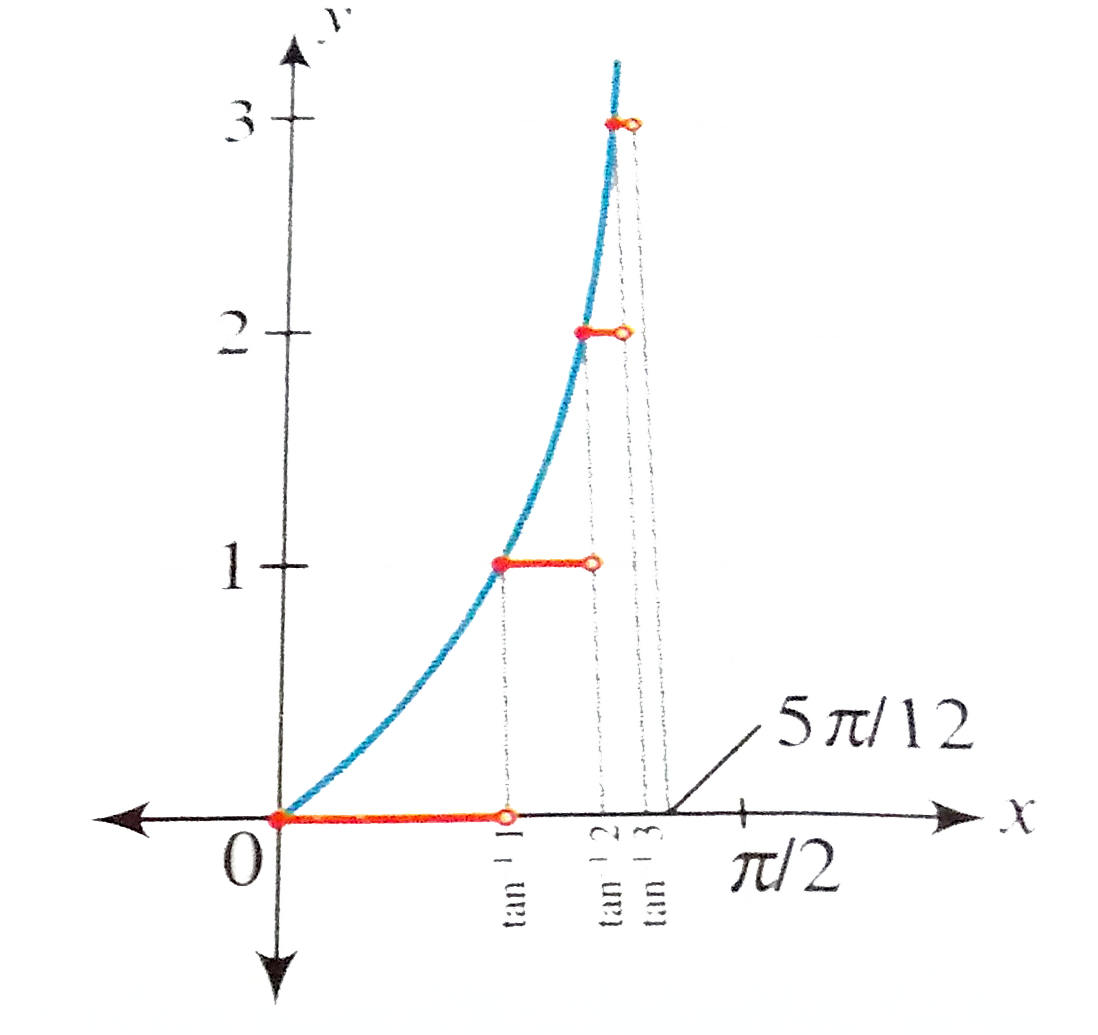
Draw the graph of f(x)=[tanx],0≤x≤5π/12, where [⋅] represents the greatest integer function.
f(x)=[tanx]
tan x is an increasing function in [0,5π/12]
tan 0 = 0 and tan(5π/12)=2+√3
Now [tan x] is discontinuous when tan x is an integer.
So f(x) is discontinuous when tanx=1,2,3(<2+√3)
∴ x=tan−11,tan−12,tan−13
f(x)=[tanx]=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩0, tanx∈[0, 1)orx∈[0,tan−11)1, tanx∈[1, 2)orx∈[tan−11,tan−12)2, tanx∈[2, 3)orx∈[tan−12,tan−13)3, tanx∈[3, 2+√3)orx∈[tan−13,5π/12)
So the graph of the function is as shown in the following figure.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Draw the graph of f(x)=[logex],e−2<x<10, where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=[sinx],x∈[0,2π], where [⋅] represents the greatest integer function.
View SolutionSolve tanx=[x],x∈(0,3π/2). Here [.] represents the greatest integer function.
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionDraw the graph of y=[cosx],x∈[0,2π], where [⋅] represents the greatest integer function.
View SolutionDraw the graph of y=sinx and y=cosx,0≤x≤2π
View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
View SolutionDraw the graph of |y|=[x], where [.] represents the greatest integer function.
View SolutionDraw the graph and discuss the continuity of f(x)=[sinx+cosx],x∈[0,2π), where [.] represents the greatest integer function.
View SolutionDraw the graph of f(x)=[x2],x∈[0,2), where [⋅] denotes the greatest integer function.
View Solution
