Find the number of solutions to loge|sinx|=−x2+2x in [−π2,3π2].
Text Solution
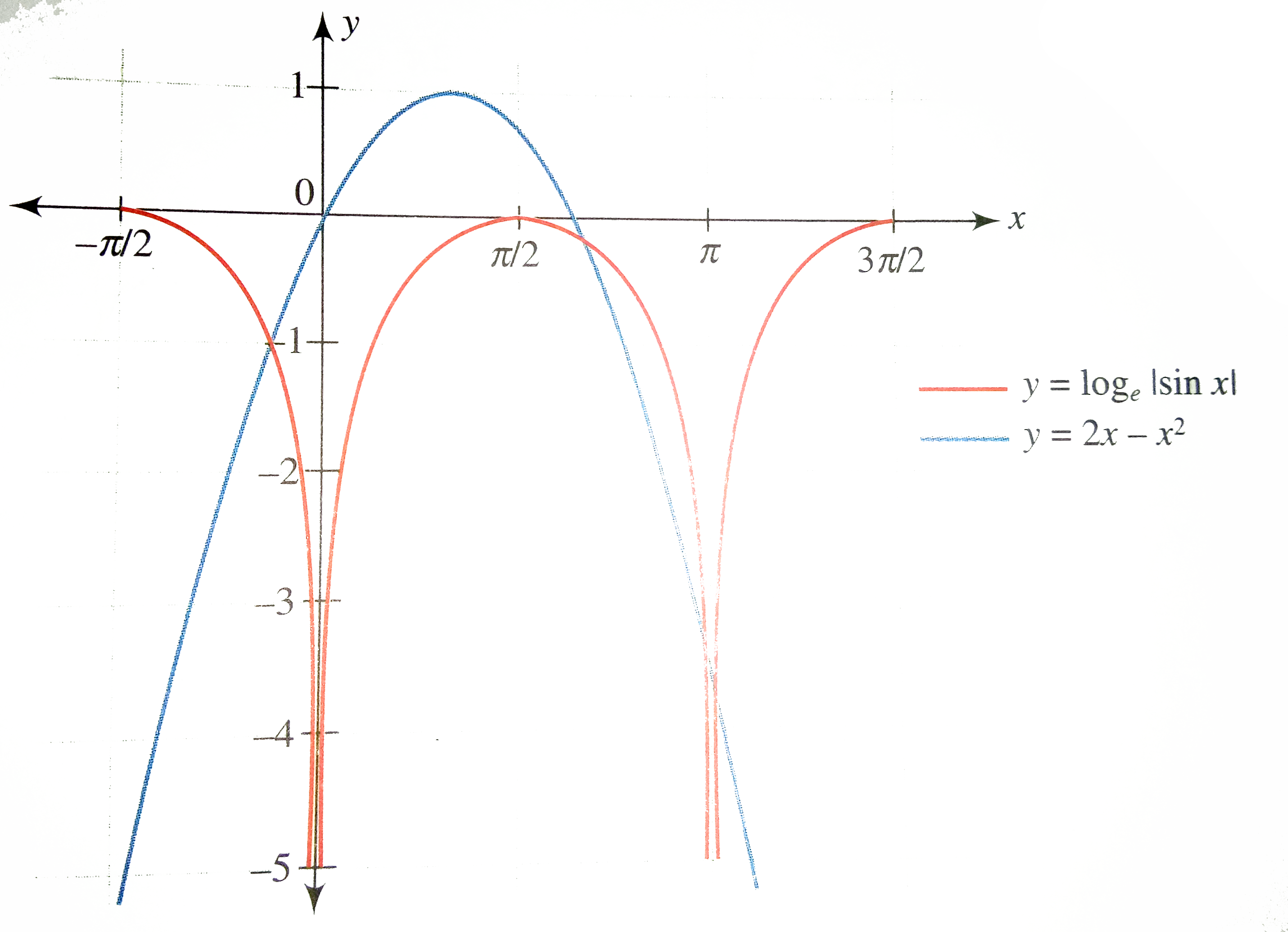
loge|sinx|=−x(x−2)
Graphs of y=loge|sinx| and y=−x(x−2) meet exactly four times in [−π2,3π2],
hence four roots.
|
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Knowledge Check
Number of solutions (s) of in |sinx|=−x2 if x∈[−π2,3π2] is/are:
A2B4C6D8Find the number of solution of log12|sinx|=2−log12|cosx|,x∈[0,2π]
A2B4C6D8
Find the number of solution of log12|sinx|=2−log12|cosx|,x∈[0,2π]
View SolutionFind the number of solution of log12|sinx|=2−log12|cosx|,x∈[0,2π]
View SolutionThe total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionThe total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionThe total number of solutions of loge|sinx|=−x2+2x∈[0,π] is equal to
View SolutionFind the total number of solutions of sinπx=|ln|x∣∣
View Solution
