If the area bounded by the curve y=x2+1 and the tangents to it drawn from the origin is A, then the value of 3A is__-
Video Solution
Text Solution
The correct Answer is:2
Let the point of the curve be (x,x2+1).
Now, the slope of tangent at this point is 2x, which is equal to the slope of the line joining (x,x2+1)and(0,0).
Hence, 2x=(x2+1)/xor2x2=x2+1
or x2+1orx=±1
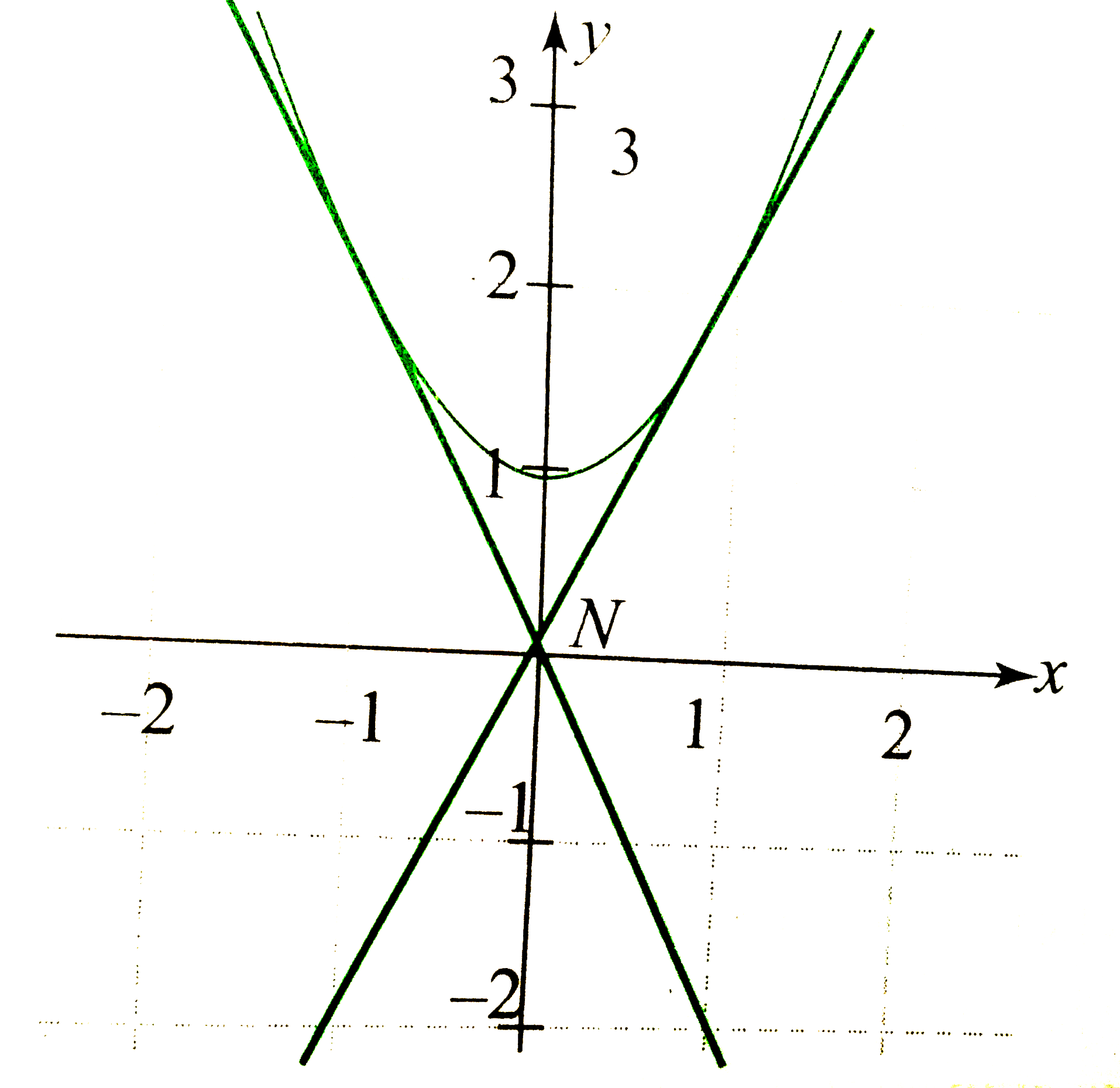
Hence, equation of tangent is y=±2x
Now Area 21∫0(x2+1−2x)dx=21∫0(x−1)2dx=2[(x−1)33]10=2/3
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Archives10videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Single Correct Answer Type30videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Matrix Match Type5videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type5videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
Similar Questions
The area bounded by the curve y=4x−x2 and the x-axis is:
View SolutionThe area bounded by the curves y=x,y=x3 is
View SolutionIf the area bounded by the curve y+x2=8x and the line y=12 is K sq. units, then the vlaue of 3K10 is
View SolutionArea bounded by the curves y=x2−1andx+y=3 is:
View SolutionThe area bounded by the curve y=x2+2x+1, the tangent at (1,4) and the y-axis is
View SolutionFind the area bounded by the curve y=x3−3x2+2x and the x-axis.
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionFind the area bounded by the curves x+2|y|=1 and x=0 .
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is
View Solution
